КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Представление сигналов в виде ряда Котельникова.
В теории и технике сигналов широко используется теорема Котельникова (теорема отсчетов): если наивысшая частота в спектре функции s (t) меньше, чем fт, то функция s (t) полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга не более чем на 1/2fт секунд.
В соответствии с этой теоремой сигнал s(t), ограниченный по спектру наивысшей частотой 
, можно представить рядом
. (1.166)
В этом выражении 1/2fm = Δt обозначает интервал между двумя отсчетными точками на оси времени, а s(n/2fm) = s (nΔt) — выборки функции s(t) в моменты времени t = nΔt.
Рис. 1.24. Представление сигнала рядом Котельникова
Представление заданной функции s(t) рядом (1.166) иллюстрируется рис. 1.24.
Функция вида
(1.167)
обладает следующими свойствами:
а) в точке t=nΔt - φn(nΔt) = 1, а в точках t=kΔt, где k — любое целое положительное или отрицательное число, отличное от п, φn (kΔt)=0;
б) спектральная плотность функции φ0(t) равномерна в полосе частот |ω|< ωт и равна 1/2fm — π/ωm.
Так как функция φn(t) отличается от φ0(t) только сдвигом на оси времени на пΔt, то спектральная плотность функции φп (t)
(1.168)
Модуль этой функции изображен на рис. 1.25, б.
То, что ряд (1.166) точно определяет заданный сигнал s(t) в точках отсчета, не требует дополнительных доказательств, поскольку коэффициентами ряда являются сами выборки из функции, т. е. величины s(nΔt). Можно доказать, что ряд (1.166) определяет функцию s(t) в любой момент t, а не только в точках отсчета t — nΔt. Воспользуемся для этого общими правилами разложения функции по ортогональной системе. В данном случае разложение производится по функциям вида (1.167), для которых интервал ортогональности равен бесконечности, а норма 
:
Рис.1.25. Связь между спектром сигнала s(t) и спектром базисной функции φn(t)
Не предрешая заранее значения коэффициентов ряда (1.166), применяем для их определения общую формулу, справедливую для обобщенного ряда Фурье
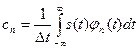(1.169)
При этом исходим из условия, что s(t) — квадратично-интегрируемая функция (энергия сигнала конечна).
Для вычисления интеграла в выражении (1.169) воспользуемся формулой 
(1.170)
Пределы интегрирования здесь приведены в соответствии с заданной граничной частотой ωm=2πfm в спектре сигнала, а также в спектре функции φn(t).
Интеграл в правой части (1.169) с коэффициентом 1/2π есть не что иное, как значение s(t) в момент t = nΔt. Таким образом, 
Подставляя этот результат в (1.170), получаем окончательное выражжение 
,
из которого следует, что коэффициентами ряда (1.166) являются выборки функции s(t) в точках t = nΔt.
Поскольку ограничение спектра конечной наивысшей частотой обеспечивает непрерывность функции s(t), ряд (1.166) сходится к функции s(t)при любом значении t.
Дата добавления: 2015-04-21; просмотров: 321; Мы поможем в написании вашей работы!; Нарушение авторских прав |