Гармонический анализ периодических сигналов.

Использование рядов Фурье для гармонического анализа сложных периодических сигналов в сочетании с принципом наложения пред­ставляет собой эффективное средство для изучения влияния линейных систем на прохождение сигналов. 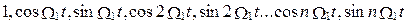Или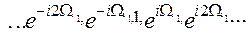

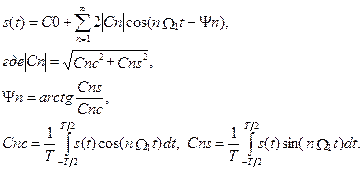Интервал ортогональности в обоих случаях совпадает с периодом 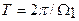функции s(t).

Система функций (1) приводит к тригонометрической форме ряда Фурье, а система (2) — к комплексной форме.

При переходе к тригонометрической форме ряд Фурье должен быть записан следующим образом:

Вместо математической формы записи в радиотехнической литературе часто встречается следующая форма записи: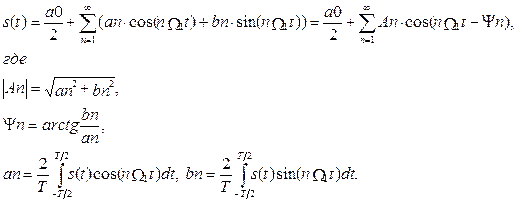

Из сопоставления выражений видно, что комплекс­ная амплитуда n-й гармоники А_п связана с коэффициентом с_п ряда , соотношением А_n = 2с_n, а а_n = 2с_nс, b_п = 2с_ns.

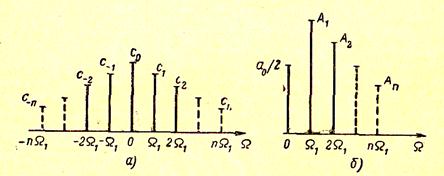
Рис.1.Спектр амплитуд.

Если сигнал представляет собой функцию, четную относительно t, т.е. s(t) = s(-t), в тригонометрической записи ряда остаются только косинусоидальные члены, так как коэффициенты b_n в соответствии с формулой (4) обращаются в нуль. Для нечетной относительно tфункции s(t), наоборот, в нуль обращаются коэффициенты а_пи ряд со­стоит только из синусоидальных членов.

Две характеристики — амплитудная и фазовая, т. е. модули и ар­гументы комплексных коэффициентов ряда Фурье, полностью определяют структуру частотного спектра периодического сигнала. На­глядное представление о «ширине» спектра дает графическое изобра­жение спектра амплитуд. В качестве примера на рис.1.а)построен спектр коэффициентов с_n, а на рис.1.б)— спектр амплитуд А_п=2∙ с_n для одного и того же периодического сигнала. Для исчерпы­вающей характеристики спектра подобные построения должны быть дополнены заданием начальных фаз отдельных гармоник.

Спектр периодической функции называется линейчатым или дискретным, так как состоит из отдельных «линий», соответ­ствующих дискретным частотам: 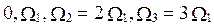и т. д.