Спектральное представление детерминированных сигналов.

Любой периодический сигнал можно рассматривать как бесконечную сумму гармоник. Удобно представить эту сумму в виде зависимости модуля амплитуды гармоники от частоты. Такое частотное распределение амплитуд гармоник, имеющее дискретный вид для периодического сигнала (рис. 1.2), на­зывается амплитудно-частотной характеристикой (АЧХ) спектра этого сиг­нала.

Рис. 1.2. Пример амплитудно-частотной характеристики периодического (А - модуль амплитуды гармоник, v - частота гармоник)

Для непериодического сигнала расстояние между спектральными линия­ми становится равным нулю, АЧХ имеет вид непрерывной функции (рис. 1.3).

Рис. 1.3. Пример АЧХ апериодического сигнала

Каждая частотная составляющая периодического сигнала в общем случае имеет фазовый сдвиг, т. е. смещение начала гармоники относительно точки, принятой за нулевую. Это смещение выражается в угловой мере (радианах, градусах). Его можно оценивать фазо-частотной характеристикой (ФЧХ). Понятие ФЧХ распространяется и на непериодические сигналы.

Вся информация как о модуле амплитуды, так и о фазе частотных состав­ляющих содержится в функции, называемой спектральной плотностью сиг­нала [1].

Спектральная плотность S(v) сигнала связана с сигналом E(t) прямым преобразованием Фурье:

и наоборот, сигнал L(t) может быть найден по его спектральной плотности S(v) обратным преобразованием Фурье:

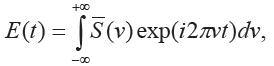
По формуле Эйлера

Используя формулу Эйлера , спектральную плотность S(v), опреде­ляемую выражением , можно представить как алгебраическую сумму вида:

где A(v) и B(v) - соответственно косинус- и синус-преобразования Фурье, рассчитываемые по формулам

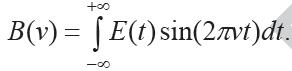
Спектральную плотность S(v) можно также выразить через две другие частотные характеристики: амплитудно-частотную S(v) и фазо-частотную ФЧХ О(v) .

Сигнал E(t) можно найти, зная его АЧХ S(v) и ФЧХ О(v):

Значение спектральной плотности S(v) и АЧХ S(v) на нулевой частоте есть интеграл вида

а ФЧХ О(v) обращается в нуль: