Спектральное представление непериодических сигналов.

Гармонический анализ периодических сигналов нетрудно распространить на непериодический сигнал. Пусть такой сигнал s(t) задан в виде некоторой функции, отличной от нуля в про­межутке t1, t2 (рис.1).

Рис.1

Выделив произвольный отрезок времени Т, включающий в себя промежуток t1, t2 мы можем представить заданный сигнал в виде ряда

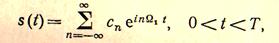(1.1)

где (1.2)

Подставив (2) в (1) получим

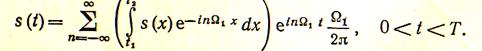(1.3)

Вне промежутка 0, Т ряд (1.3) определяет функцию s(t)=s(t±kT), где k— целое число, т. е. периодическую функцию, полученую повторением s(t)) вправо и влево с периодом Т, Для юго чтобы вне этрезка 0, Т функция равнялась нулю, величина Т должна быть бесконечно большой, Но чем больше отрезок Т, выбранный в качестве пеиода, тем меньше коэффициенты с_п. Устремляя Т к бесконечности, пределе получаем бесконечно малые амплитуды гармонических сотавляющих, сумма которых изображает исходную непериодическую функцию s(t), заданную в интервале и t1<t < t2(рис.1). Количество гармонических составляющих, входящих в ряд Фурье, будет при этом бесконечно большим, так как при Т=∞ основная частота функции Ω1 =0. Иными словами, расстояние между спектральными линиями, равное основной частоте Ω1, становится бес­конечно малым, а спектр — сплошным.

Можно поэтому в выражении (1.3) заменить Ω1 на d Ω, n Ω1 на текущую частоту Ω , а операцию суммирования — на операцию интег­рирования.

Таким образом приходим к двойному интегралу Фурье:

Внутренний интеграл, являющийся функцией Ω

называется спектральной плотностью или спектральной характеристикой функции s(t).