Дифференциальные уравнения движения свободной и несвободной МТ. Две задачи динамики точки

Используя основной закон динамики и формулы для ускорения МТ при различных способах задания движения, можно получить дифференциальные уравнения движения как свободной, так и несвободной материальной точки. При этом для несвободной материальной точки ко всем приложенным к МТ активным (заданным) силам надо добавить на основании аксиомы связей (принципа освобождаемости) силы пассивные (реакции связи).

Пусть 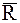– равнодействующая системы сил (активных и реакций), действующих на точку.

На основании второго закона динамики

(1)

с учетом соотношения, определяющего ускорение точки при векторном способе задания движения:

,

получим дифференциальное уравнение движения МТ постоянной массы в векторной форме:

. (2)

Спроектировав соотношение (1) на оси декартовой системы координат Oxyz и использовав соотношения, определяющие проекции ускорения на оси декартовой системы координат:

, , ,

получим дифференциальные уравнения движения МТ в проекциях на эти оси:

(3)

Спроектировав соотношение (1) на оси естественного трехгранника ( ) и использовав соотношения, определяющие формулы для ускорения точки при естественном способе задания движения:

, , ,

получим дифференциальные уравнения движения МТ в проекциях на оси естественного трехгранника :

(4)

Аналогично можно получить дифференциальные уравнения движения МТ в других системах координат (полярной, цилиндрической, сферической и т. д.).

С помощью уравнений (2)-(4) ставятся и решаются две основные задачи динамики МТ

Первая (прямая) задача динамики МТ: зная массу МТ и заданные тем или иным способом уравнения или кинематические параметры ее движения, необходимо найти действующие на МТ силы.

Например, если заданы уравнения движения МТ в декартовой системе координат:

то проекции на оси координат силы 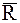, действующей на МТ, определятся после использования соотношений (3):

Зная проекции силы на координатные оси, легко определить модуль силы и направляющие косинусы углов, которые составляет сила с осями декартовой системы координат.

Для несвободной МТ обычно необходимо еще, зная действующие на нее активные силы, определить реакции связи.

Вторая (обратная) задача динамики МТ: зная массу точки и действующие на нее силы, необходимо определить уравнения или кинематические параметры ее движения при определенном способе задания движения.

Для несвободной МТ обычно необходимо, зная массу МТ и действующие на нее активные силы, определить уравнения или кинематические параметры ее движения и реакции связи.

Силы, приложенные к точке, могут зависеть от времени, положения МТ в пространстве и от скорости ее движения, т. е.

.

Рассмотрим решение второй задачи в декартовой системе координат. Правые части дифференциальных уравнений движения (3) в общем случае содержат функции времени, координат, их производных по времени:

(5)

Для того, чтобы найти уравнения движения МТ в декартовых координатах, необходимо дважды проинтегрировать систему трех обыкновенных дифференциальных уравнений второго порядка (5), в которых неизвестными функциями являются координаты движущейся точки, а аргументом – время t. Из теории обыкновенных дифференциальных уравнений известно, что общее решение системы трех дифференциальных уравнений второго порядка содержит шесть произвольных постоянных:

(6)

где C_g, (g = 1,2,…,6) – произвольные постоянные.

Продифференцировав соотношения (6) по времени, определим проекции скорости МТ на координатные оси:

(7)

В зависимости от значений постоянных C_g, (g =1,2,…,6) уравнения (6) описывают целый класс движений, который могла бы совершить МТ под действием данной системы сил.

Действующие силы определяют только ускорение МТ, а скорость и положение МТ на траектории зависят еще от скорости, которую сообщили МТ в начальный момент, и от начального положения МТ.

Для выделения конкретного вида движения МТ (т. е. чтобы сделать вторую задачу определенной) надо дополнительно задать условия, позволяющие определить произвольные постоянные. В качестве таких условий задают начальные условия, т. е. в какой-то определенный момент времени, принимаемый за начальный, задаются координаты движущейся МТ и проекции ее скорости:

при t = 0 :

(8)

где – значения координат МТ и их производных в начальный момент времени t=0.

Используя начальные условия (8), формулы (7) и (6), получаем шесть алгебраических уравнений для определения шести произвольных постоянных:

(9)

Из системы (9) можно определить все шесть произвольных постоянных:

. (g = 1,2,…,6)

Подставляя найденные значения C_g, (g = 1,2,…,6) в уравнения движения (6), находим решения второй задачи динамики в виде закона движения точки.