Колебательное движение МТ в среде с сопротивлением при отсутствии возмущающей силы

В этом случае дифференциальное уравнение движения в проекции на ось Х примет вид:

, (1)

и решение при малом сопротивлении среды (n < w) в соответствии с формулой

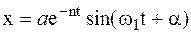, (2)

где а и a – постоянные интегрирования, которые находятся из начальных условий.

Из уравнения (2) следует, что движение МТ будет колебательным. Эти колебания называют затухающими, так как за счет множителя размахи колебаний будут убывать, стремясь с течением времени к нулю. Период затухающих колебаний

.

Графически затухающие колебания можно иллюстрировать затухающей синусоидой (Рис. 1)

Рис. 1

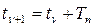Чтобы установить закон затухания размахов колебания, отметим, что промежуток времени между двумя последовательными максимальными отклонениями МТ и равен периоду Т_п, т.е. . С учетом этого найдем:

.

Отсюда следует, что наибольшие отклонения МТ убывают с течением времени по закону геометрической прогрессии, знаменатель которой называется декрементом колебаний. Соответственно величина называется логарифмическим декрементом затухания.

В случае большого сопротивления среды (n > w) движение МТ будет неколебательным (апериодическим) затухающим:

,

где – действительные отрицательные числа, а С₁ и С₂ - постоянные интегрирования, которые находятся из начальных условий.

График этого движения МТ в зависимости от величины и знака начального отклонения х₀ и направления начальной скорости 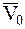имеет форму одной из кривых, изображенных на рисунке (или им симметричных относительно оси абсцисс).

Рис. 2

В предельном случае (n = w) движение МТ также будет неколебательным (апериодическим) затухающим:

,

где С₁ и С₂ – постоянные интегрирования, которые находятся из начальных условий.

Картина движения МТ будет качественно такой же, как показанная на рис. 2.