Теорема об изменении кинетической энергии МТ, работа силы

Умножив обе части основного закона динамики скалярно на 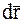, получим:

или, учитывая, что ,

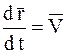. (1)

Так как , то, взяв дифференциал от обеих частей, получим:

.

Учтя, что масса постоянна, находим 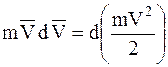, и тогда соотношение (1) примет вид:

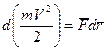(2)

или

, (3)

где правые части соотношений (2), (3) представляют собой элементарную работу силы, действующей на МТ:

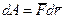. (4)

Выражения (2) или (3) представляют первую дифференциальную форму теоремы об изменении кинетической энергии МТ.

Теорема: Дифференциал кинетической энергии МТ равняется элементарной работе силы, действующей на МТ.

Поделив соотношения или (2) или (3) на dt, получим вторую дифференциальную форму теоремы об изменении кинетической энергии МТ:

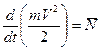, (5)

где 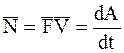является мощностью силы, действующей на МТ.

Теорема: Производная по времени от кинетической энергии МТ равняется мощности силы, приложенной к МТ.

Если рассмотреть конечное перемещение МТ из одного положения (1), где ее скорость равна 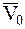в другое положение (2), где ее скорость равна , то, беря от обеих частей равенства (3) соответствующие интегралы, получим:

. (6)

Соотношение (6) выражает теорему об изменении кинетической энергии МТ в конечной (интегральной) форме.

Теорема: Изменение кинетической энергии МТ на конечном перемещении равняется работе силы, действующей на МТ на том же перемещении.

В соотношении (6) правая часть представляет собой работу силы, действующей на МТ на конечном перемещении:

. (7)

Учитывая, что 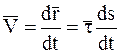, т. е. , преобразуем выражение (7)

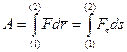. (8)