
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Эллипсоид инерции, главные оси инерции
Для характеристики распределения моментов инерции СМТ относительно различных осей, проходящих через заданную точку, используется поверхность второго порядка – эллипсоид инерции. Для построения этой поверхности на каждой осиl, проходящей через точку 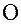 , откладывается вектор
, откладывается вектор  , модуль которого равен:
, модуль которого равен:
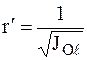 . (1)
. (1)
Здесь
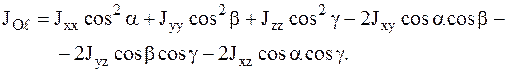 (2)
(2)
Выразим косинусы углов  через координаты
через координаты  вектора
вектора  :
:
 (3)
(3)
Подставив в соотношение (2) формулы (3), получим уравнение поверхности второго порядка:
 . (4)
. (4)
Геометрическое место концов вектора  располагается на поверхности, которая называется эллипсоидом инерции. Для каждой точки O имеется свой эллипсоид инерции. Эллипсоид инерции для центра масс СМТ называется центральным эллипсоидом инерции. Оси эллипсоида инерции называются главными осями инерции. В общем случае эллипсоид инерции имеет три взаимно перпендикулярные главные оси инерции. Они являются его осями инерции.
располагается на поверхности, которая называется эллипсоидом инерции. Для каждой точки O имеется свой эллипсоид инерции. Эллипсоид инерции для центра масс СМТ называется центральным эллипсоидом инерции. Оси эллипсоида инерции называются главными осями инерции. В общем случае эллипсоид инерции имеет три взаимно перпендикулярные главные оси инерции. Они являются его осями инерции.
Моменты инерции относительно главных осей инерции называются главными моментами инерции, а относительно главных центральных осей инерции – главными центральными моментами инерции.
Если уравнение эллипсоида инерции отнести к его главным осям Ox', Oy', Oz', то оно примет вид:
 , (5)
, (5)
где x', y', z'– текущие координаты точки, расположенной на эллипсоиде инерции, относительно главных осей инерции;  – главные моменты инерции.
– главные моменты инерции.
Центробежные моменты инерции относительно главных осей инерции равны нулю
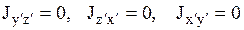 .
.
Дата добавления: 2015-04-21; просмотров: 310; Мы поможем в написании вашей работы!; Нарушение авторских прав |