Теорема о движении центра масс СМТ

Считая, что массы МТ постоянны, преобразуем формулу, определяющую количество движения СМТ, следующим образом:

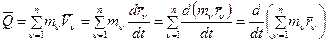. (1)

На основании определения центра масс 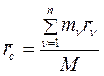, поэтому:

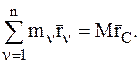(2)

Подставляя соотношение (2) в (2), получим:

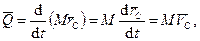
Таким образом, количество движения СМТ равно количеству движения, которое имел бы центр масс СМТ, если бы в нем была сосредоточена вся масса СМТ

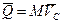. (3)

Подставляя (3) в теорему об изменении количества движения СМТ

получим теорему о движении центра масс СМТ в векторной форме:

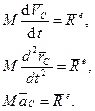(4)

Теорема: Центр масс СМТ движется как МТ, в которой сосредоточена вся масса СМТ и к которой приложены все внешние силы, действующие на СМТ.

Проектируя второе соотношение формул (4) на оси декартовой системы координат, получим дифференциальные уравнения движения центра масс СМТ в проекциях на оси декартовой системы координат:

(5)

Из теоремы о движении центра масс СМТ можно получить два следствия, аналогичные закону сохранения количества движения СМТ.

Следствия:

· Если 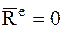, то из первого соотношения формул (4) следует, что

.

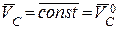Если главный вектор внешних сил, действующих на СМТ, равен нулю, то СМТ движется так, что скорость центра масс СМТ постоянна по величинеи направлению и равна скорости центра масс в начальный момент времени.

Если (для определенности выбрана ось х), то из первого соотношения уравнений (5) следует, что

.

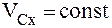Если проекция главного вектора внешних сил СМТ на какую-либо ось равна нулю, то СМТ движется так, что проекция скорости центра масс СМТ на эту ось является постоянной величиной и равна проекции скорости центра масс на эту ось в начальный момент времени.