Кинетическая энергия НМС в частных случаях движения. Теорема Кенига

· Поступательное движение НМС.

В случае поступательного движения НМС все ее точки движутся с одинаковыми скоростями, равными скорости движения центра масс НМС: ,поэтому по определению для Т получим

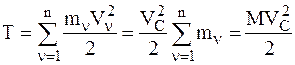. (1)

· Вращательноедвижение НМС вокруг неподвижной оси z.

В случае вращательногодвижения НМС все ее МТ движутся со скоростями 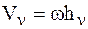, где 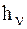- кратчайшее расстояние от n-й МТ до оси вращения. Соотношение, определяющее Т в случае вращательногодвижения НМС вокруг неподвижной оси z примет вид:

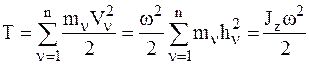. (2)

· Плоскопараллельноедвижение НМС.

В случае плоскопараллельногодвижения НМС в каждый момент времени движение НМС можно рассматривать как мгновенное вращательное движение относительно оси, перпендикулярной неподвижной (основной) плоскости и проходящей через мгновенный центр скоростей . Поэтому можно использовать соотношение (2)

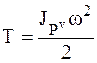, (3)

где 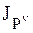– момент инерции НМС относительно мгновенной оси, перпендикулярной к неподвижной плоскости движения и проходящей через мгновенный центр скоростей.

Используем теорему Штейнера-Гюйгенса:

,

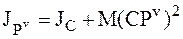где J_С – момент инерции НМС относительно мгновенной оси, перпендикулярной к неподвижной плоскости движения и проходящей через центр масс С, а СР^v – расстояние между мгновенным центром скоростей и центром масс.

Подставив это выражение в соотношение (3), получим:

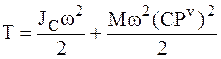или

, (4)

где – скорость центра масс НМС.

Теорема Кенига:Кинетическая энергия СМТ в общем случае движения равна сумме кинетической энергии центра масс в предположении, что в нем сосредоточена вся масса СМТ, и кинетической энергии СМТ при ее движении относительно подвижной системы отсчета, перемещающейся вместе с центром масс поступательно.