Плоскопараллельного движения НМС

Дифференциальные уравнения поступательного движения

Изучение кинематики поступательного движения НМС показало, что исследование поступательного движения НМС сводится к рассмотрению движения любой ее МТ. Взяв в качестве такой МТ центр масс С, на основании теоремы о движении центра масс можно записать дифференциальные уравнения поступательного движения НМС в виде:

(1)

При движении центра масс НМС в одной плоскости, например xOy, дифференциальные уравнения поступательного движения НМС будут представлены двумя первыми уравнениями из соотношений (1).

Дифференциальное уравнение вращательного движения НМС относительно неподвижной оси

Пусть на НМС, имеющую неподвижную ось вращения z и оси х и у жестко связанных с НМС, действует система внешних сил . Использовав принцип освобождаемости, заменим действие связей в подпятнике О и подшипнике В силами реакции связи и (рис1).

Чтобы получить дифференциальное уравнение вращательного движения НМС относительно неподвижной оси Оz, применим теорему об изменении кинетического момента СМТ относительно оси вращения Oz:

.

Рис. 1

Так как реакции и пересекают ось z, то

и, следовательно,

. (2)

Найдем кинетический момент НМС, вращающейся относительно неподвижной оси Оz (рис2)

.

Скорость n-й точки НМС, вращающейся относительно неподвижной оси, определится соотношением:

,

где w – угловая скорость НМС, а h_n – расстояние от n-й точки НМС до оси z.

Момент количества движения n-й МТ относительно оси Oz примет вид:

.

рис2

Тогда кинетический момент НМС относительно неподвижной оси определится из соотношения:

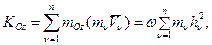
здесь – момент инерции НМС относительно оси Oz.

Окончательно для кинетического момента НМС, вращающейся относительно неподвижной оси, имеем:

.

Подставляя в уравнение (2) найденное значение кинетического момента НМС, получим:

.

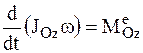Для НМС момент инерции J_Оz = const и, следовательно,

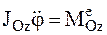, , . (3)

Уравнения (3) представляют собой различные формы записи уравнения вращательного движения НМС вокруг неподвижной оси.

На основании третьего соотношения (3) можно сделать вывод, что при данном значении вращательного момента , чем больше – момент инерции НМС относительно оси вращения, тем меньше e – угловое ускорение НМС и наоборот. Следовательно, момент инерции является мерой инертности НМС при ее вращательном движении вокруг неподвижной оси Оz.

Дифференциальные уравнения плоскопараллельного движения НМС

Предположим, что НМС под действием системы внешних сил совершает плоскопараллельное движение, при котором все точки НМС движутся в плоскостях, параллельных некоторой неподвижной плоскости, в качестве которой примем координатную плоскость xOy (рис. 3).

Рис. 3

Из кинематики известно, что для определения положения НМС, совершающего плоскопараллельное движение, достаточно задать положение какой-нибудь его МТ, принятой за полюс, и угол поворота НМС вокруг оси, проходящей через этот полюс и перпендикулярной к неподвижной плоскости, параллельно которой происходит движение всех МТ рассматриваемого НМС. Задачи динамики решаются проще, если за полюс взять центр масс С и определять положение НМС координатами центра масс и углом поворота j НМС вокруг оси , проходящей через центр масс С и перпендикулярной к плоскости xOy.

Таким образом, для изучения плоскопараллельного движения свободного НМС достаточно составить три дифференциальных уравнения, связывающих величины и j с действующими на НМС внешними силами. Для описания движения центра масс воспользуемся первыми двумя уравнениями движения центра масс (1). Добавляя к ним уравнения вида (3) относительно оси Сz, получаем дифференциальные уравнения плоскопараллельного движения НМС:

(4)

Замечание: без доказательства приняли, что уравнение вращения относительно подвижной оси Oz сохраняет свой вид, как для случая вращения относительно неподвижной оси.