Классификация связей. Виртуальные перемещения.

МТ или СМТ называются свободными, если на движение МТ или точек СМТ (координаты, скорости) не наложено никаких ограничений. Ограничения, накладываемые на параметры движения МТ или точек СМТ, называются связями.

Аналитически они могут быть представлены в виде уравнений или неравенств, связывающих между собой координаты МТ или точек СМТ, их производные и время. Например, в декартовой системе координат эти условия в общем случае могут быть записаны в виде:

(1)

где – число связей, n – число точек СМТ (для МТ ).

Так как при движении МТ или СМТ координаты x, y, z и скорости являются функциями времени, то время в уравнения или неравенства связей может входить как неявно через аргументы этих функций, так и явно.

Связи называются стационарными, если они не зависят от времени, т. е. время не входит явно в уравнения или неравенства связей, и они имеют вид:

. (2)

Здесь и в дальнейшем в случае СМТ в соотношениях, описывающих связи, под х понимается совокупность x₁, x₂,…, x_n, под у совокупность у₁, у₂,…,у_n и т. д.

Связи называются нестационарными, если они зависят от времени, т. е. время входит явно в уравнения или неравенства связей, и они имеют вид (1).

Связи называются геометрическими, если ограничения накладываются только на положение МТ или точек СМТ, т. е. в уравнения или неравенства связей входят только координаты, и они имеют вид:

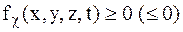
. (3)

Связи называются кинематическими, если ограничения накладываются на скорость МТ или скорости точек СМТ, т. е уравнения или неравенства связей содержат производные от координат по времени, и имеют вид (1).

Если уравнения кинематической связи могут быть проинтегрированы и заменены уравнениями, не содержащими скоростей, то такие связи называются голономными (дифференциальными интегрируемыми).

Связи называются удерживающими (неосвобождающими), если они не могут исчезать или появляться вновь, т. е. МТ или точки СМТ в процессе движения не могут покинуть связи, и они описываются уравнениями вида:

. (4)

Связи называются неудерживающимися (неосвобождающимися), если они могут исчезать или появляться вновь, т. е. МТ или точки СМТ в процессе движения могут покинуть связи, и они описываются соотношениями (1) в виде строгих или нестрогих неравенств.

Если материальная точка движется по закону или в проекциях на оси , , , 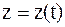то ее действительное перемещение МТ за бесконечно малый промежуток времени dt будет . Координаты вектора 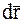(его проекции на оси декартовой системы координат) определяются из соотношений: , , . То есть координаты МТ при действительном перемещении изменяются вследствие изменения аргумента t на величину dt, математически эти изменения выражаются дифференциалами радиуса вектора и его координат.

Любое бесконечно малое перемещение, которое может быть сообщено материальной точке из занимаемого ею в данный момент времени положения при сохранении наложенных на нее связей, называется ее виртуальным (возможным) перемещением.

В отличие от действительного перемещения, совершаемого МТ за определенный промежуток времени и обусловленного приложенными к ней силами, виртуальное перемещение на самом деле не реализуются и по сути своей является воображаемым. Изменение координат МТ при виртуальном перемещении не является следствием изменения аргумента в ее законе движения, как при действительном перемещении, а обусловлено изменением вида самой функции закона движения материальной точки.

Бесконечно малое изменение функции, происходящее вследствие изменения аргумента, выражается дифференциалом этой функции. Если же изменение функций происходит вследствие изменения вида самой функции, то такое изменение называется вариацией функций и обозначается символом d. Поэтому, в отличие от действительного ( 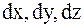), виртуальное перемещение МТ обозначается через (рис. 1), а его проекции на оси координат через .

Совокупность виртуальных перемещений точек СМТ, не нарушающих наложенных на СМТ связей, называется виртуальным перемещением СМТ.