
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнения Лагранжа второго рода (Уравнения движения СМТ в обобщенных координатах)
Используем следующую форму общего уравнения динамики:
 . (1)
. (1)
Пусть на механическую систему, имеющую m степеней свободы, наложены голономные, удерживающие и идеальные связи. Введем в рассмотрение m обобщенных координат qg (g=1,…,m) и выразим через них радиус-вектор n-й точки:
 ,
,  . (2)
. (2)
Варьируя это соотношение, получим:
 ,
,  . (3)
. (3)
Подставляя соотношение (3) в соотношение (1) и изменяя порядок суммирования, имеем:
 . (4)
. (4)
Так как все  независимы и произвольны, то равенство (4) может выполняться только тогда, когда каждый из коэффициентов при
независимы и произвольны, то равенство (4) может выполняться только тогда, когда каждый из коэффициентов при  равен нулю, поэтому находим:
равен нулю, поэтому находим:
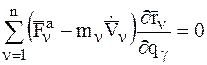 .
.  (5)
(5)
Эту систему m уравнений запишем в виде:
 .
.  (6)
(6)
Правая часть соотношения (6) представляет собой обобщенную силу  соответствующую обобщенной координате
соответствующую обобщенной координате 
 :
:
 .
.  (7)
(7)
Преобразуем выражение, входящее в левую часть соотношения (6) следующим образом:
 (8)
(8)
Учитывая, что радиус-вектор n-й МТ зависит от времени t сложным образом, получим из(2)следующее выражение для ее скорости:
 , (9)
, (9)
где  – называется обобщенной скоростью (g = 1, 2,…, m).
– называется обобщенной скоростью (g = 1, 2,…, m).
Так как множители 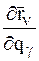 (g = 1, 2,…, m) зависят только от обобщенных координат и времени t (и не зависят от обобщенных скоростей), то дифференцируя правую и левую часть соотношения (9) по обобщенной скорости
(g = 1, 2,…, m) зависят только от обобщенных координат и времени t (и не зависят от обобщенных скоростей), то дифференцируя правую и левую часть соотношения (9) по обобщенной скорости  , приходим к соотношению:
, приходим к соотношению:
 . (10)
. (10)
Найдем частную производную скорости  по обобщенной координате
по обобщенной координате  , учитывая, что обобщенные координаты входят в правую часть равенства (9) через коэффициенты при обобщенных скоростях:
, учитывая, что обобщенные координаты входят в правую часть равенства (9) через коэффициенты при обобщенных скоростях:
 . (11)
. (11)
Частная производная  зависит от времени t явно и через обобщенные координаты
зависит от времени t явно и через обобщенные координаты  , (
, (  ). Вычисляя полную производную по времени от частной производной находим:
). Вычисляя полную производную по времени от частной производной находим:
 . (12)
. (12)
Сравнивая правые части выражений (11) и (12), замечаем, что
 . (13)
. (13)
Возвращаясь к формуле (8) и подставляя в нее тождества (19) и (13), получаем:
 . (14)
. (14)
Учитывая, что
 и
и 
приведем последнее равенство к виду:
 . (15)
. (15)
Кинетическая энергия системы определяется формулой:
 ,
,
тогда (15) примет вид:

 . (16)
. (16)
Подставляя выражения (7) и (16) в уравнения (6), получим:

 . (17)
. (17)
(17)- уравнения Лагранжа второгорода. Число уравнений Лагранжа второго рода равно числу независимых обобщенных координат, т. е. числу степеней свободы этой голономной системы.
Кинетическая энергия системы при подстановке в эти уравнения должна быть предварительно выражена как функция обобщенных скоростей  и координат
и координат  . Это будет квадратичная функция обобщенных скоростей
. Это будет квадратичная функция обобщенных скоростей  , в коэффициенты которой могут входить обобщенные координаты
, в коэффициенты которой могут входить обобщенные координаты  (в частных случаях кинетическая энергия может быть квадратичной функцией скоростей с постоянными коэффициентами). Обобщенные силы
(в частных случаях кинетическая энергия может быть квадратичной функцией скоростей с постоянными коэффициентами). Обобщенные силы  тоже могут быть в общем случае функциями обобщенных координат
тоже могут быть в общем случае функциями обобщенных координат  , и скоростей
, и скоростей  . Таким образом, в выражения
. Таким образом, в выражения  ,
,  и
и  могут входить обобщенные координаты
могут входить обобщенные координаты  и их производные
и их производные  . Поэтому в выражение
. Поэтому в выражение 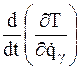 войдут уже вторые производные
войдут уже вторые производные  . Следовательно, уравнения Лагранжа второго рода (3.18) представляют собой обыкновенные дифференциальные уравнения второго порядка относительно обобщенных координат
. Следовательно, уравнения Лагранжа второго рода (3.18) представляют собой обыкновенные дифференциальные уравнения второго порядка относительно обобщенных координат 
 .
.
Дата добавления: 2015-04-21; просмотров: 295; Мы поможем в написании вашей работы!; Нарушение авторских прав |