Теоремы об изменении количества движения, о движении центра масс и об изменении кинетического момента СМТ при ударе

Рассмотрим СМТ, состоящую из n МТ, и выделим n-ю МТ с массой .

Так же как при доказательстве общих теорем динамики СМТ, разделим все ударные импульсы, действующие на МТ, на внешние и внутренние. Тогда основное уравнение теории удара для n-й МТ рассматриваемой СМТ примет вид:

, (1)

где и – скорости n-й МТ соответственно в конце удара и в начале удара, – равнодействующая всех внешних ударных импульсов, приложенных к n-й МТ, а – равнодействующая всех внутренних ударных импульсов, приложенных к той же МТ.

Составив такие уравнения для всех n МТ рассматриваемой СМТ и сложив их почленно, получим:

.

Введя следующие обозначения: 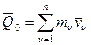– количество движения СМТ до удара, – количество движения СМТ после удара и учтя, что , так как внутренние ударные импульсы на основании третьего закона динамики - закона равенства действия и противодействия попарно равны по модулю и противоположны по направлению, получим:

. (2)

Теорема об изменении количества движения СМТ при ударе: Изменение количества движения СМТ за время удара равно геометрической сумме всех внешних ударных импульсов, действующих на эту СМТ.

Поскольку количество движения СМТ равно произведению массы CМТ на скорость центра масс СМТ, то уравнению (2) можно придать иную форму:

, (3)

где М – масса СМТ, а – скорости центра масс СМТ в начале и в конце удара.

Уравнение (3) выражает теорему о движении центра масс СМТ при ударе: изменение при ударе количества движения центра масс СМТ, в котором сосредоточена вся ее масса, равно геометрической сумме импульсов всех внешних ударных сил, действующих на СМТ.

Снова рассмотрим основное уравнение теории удара (1) для n-й точки.

Обозначим радиус-вектор n-й точки СМТ относительно начала О инерциальной системы координат через .Поскольку положение n-й точки за время удара не изменится, то за это время не изменится и ее радиус-вектор .

Составив такие же уравнения (1) для всех n МТ рассматриваемой СМТ, а затем умножив обе части равенств векторно слева на радиус-вектор и сложив их почленно, получим:

Введем следующие обозначения:

, – кинетические моменты СМТ относительно центра О соответственно до и после удара.

Так как внутренние ударные импульсы равны по модулю и противоположны по направлению, то геометрическая сумма их моментов относительно любого центра равна нулю. Поэтому полученное уравнение с учетом обозначений примет вид:

(4)

Уравнение (4) выражает теоремуоб изменении кинетического момента СМТ при ударе: изменение за время удара кинетического момента СМТ относительно какого-нибудь неподвижного центра равно геометрической сумме моментов импульсов внешних ударных сил, действующих на СМТ, относительно того же центра.