Уравнения Лагранжа в случае потенциальных сил. Циклические координаты и циклические интегралы

В случае потенциальных сил обобщенные силы определяются через потенциальную энергию системы соотношениями:

.

Тогда уравнения Лагранжа

.

перепишутся в виде:

.

Введем функцию Лагранжа 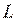соотношением: .

Учитывая, что потенциальная энергия есть функция только обобщенных координат:

,

имеем:

.

Если в функцию Лагранжа не входят явно обобщенных координат , то возможно частичное интегрирование дифференциальных уравнений движения механической системы. Соответствующие обобщенные координаты называются циклическими. Для них:

.

Тогда откуда находим общих, так называемых циклических интегралов системы дифференциальных уравнений движения механической системы:

Основные понятия и гипотезы теории удара. Основное уравнение теории удара

Явление, при котором за малый промежуток времени, т.е. почти мгновенно, скорости точек материальных объектов изменяются на конечные величины, называется ударом.

Так как при ударе конечное изменение скоростей происходит за весьма малый промежуток времени, то при этом возникают очень большие ускорения, а, следовательно, и очень большие силы. Эти силы действуют в течение весьма малого промежутка времени, но их импульсы за этот промежуток времени являются конечными величинами.

Силы, возникающие при ударе в течение малого промежутка времени, но достигающие при этом большой величины, так что их импульсы за этот промежуток времени являются конечными величинами, называются ударными силами.

Малый промежуток времени, в течение которого длится удар, называется временем удара. Импульсы ударных сил за время удара называются ударными импульсами.

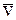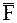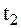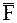Пусть дана МТ массы m, которая движется под действием обычной (неударной) силы . В момент , когда рассматриваемая МТ имеет скорость – скорость до удара, на нее начинает действовать ударная сила , действие которой прекращается в момент . Определим движение МТ под действием сил и за время удара .

Применяя теорему об изменении количества движения точки, получим:

,

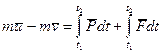где – скорость точки в момент 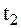после удара.

По теореме о среднем значении определенного интеграла можно написать:

,

где и есть средние значения сил 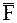и в некоторый промежуток времени. При этом является конечной величиной; ударная сила 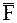за время удара достигает весьма большой величины (порядка 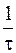). Поэтому произведение 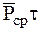будет пренебрежимо мало по сравнению с произведением , являющимся величиной конечной.

Итак, импульсами неударных сил за время удара будем пренебрегать по сравнению с импульсами ударных сил.

Окончательно получим:

. (1)

В рассматриваемой элементарной теории удара (1) принимается в качестве основного уравнения: Изменение количества движения МТ за время удара равно действующему на эту МТ ударному импульсу.

(1) играет такую же роль в теории удара, как второй закон динамики при изучении движений под действием обычных сил.

Проектируя векторное равенство (1) на координатные оси, получим три следующих уравнения:

(2)

Определим перемещение точки за время удара.

Так как , где – радиус-вектор, определяющий положение данной МТ относительно некоторой системы отсчета, то уравнение (1) можно записать следующим образом:

Проинтегрировав это равенство в пределах от до 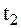, найдем:

,
где есть среднее значение ударного импульса за время удара . Учитывая при этом, что 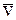и суть величины конечные, а 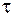- весьма мало, приходим к выводу, что будет близко к нулю и, следовательно, за время удара перемещение МТ практически равно нулю.

Таким образом, перемещением МТ за время удара можно пренебречь