Общее уравнение динамики (принцип Даламбера-Лагранжа)

Пользуясь принципом Даламбера, можно придать уравнениям движения форму уравнений равновесия, если к активным (заданным) и пассивным (реакции связей) силам присоединить силы инерции.

Пусть имеется СМТ с удерживающими и идеальными связями. Тогда для каждой МТ, входящей в СМТ, согласно принципу Даламбера можно записать:

(1)

Сообщив МТ, входящим в СМТ, виртуальные перемещения , умножим каждое из уравнений (1) на соответствующее , (n=1,2,…,n) и сложим полученные выражения:

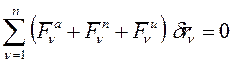. (2)

Так как связи, наложенные на систему, идеальные, то выполняются условия

(3)

и из (2) получаем общее уравнение динамики

. (4)

Общее уравнение динамикиутверждает (принцип Даламбера-Лагранжа): При движении механической системы с удерживающими и идеальными связями, сумма элементарных работ всех активных сил, действующих на точки системы и условно приложенных к ним сил инерции на любом виртуальном перемещении равна нулю.

Общее уравнение динамики можно представить также в виде:

(5)

Принцип виртуальных перемещений является частным случаем общего уравнения динамики (в случае равновесия механической системы сила инерции ).