
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Принцип Даламбера для материальной точки и механической системы. Уравнения метода кинетостатики
Основное уравнение динамики точки:
 (1)
(1)
 Перенесем произведение массы на ускорение в правую часть:
Перенесем произведение массы на ускорение в правую часть: 

Получившееся дополнительное слагаемое имеет размерность силы и принимается
за силу инерции, направленную в сторону противоположную ускорению:
 (2)
(2)
С введением силы инерции уравнение динамики точки принимает вид уравнения равновесия:
 (3)
(3)
Принцип Даламбера для материально точки:
Геометрическая сумма приложенных к точке сил и силы инерции этой точки равна нулю.
Для несвободной материально точки под  следует понимать не только активные силы, но и реакции связей (по аксиоме связей).Сила инерции условно добавляется к действующим на точку силам, образуя взаимно уравновешенную систему сил.
следует понимать не только активные силы, но и реакции связей (по аксиоме связей).Сила инерции условно добавляется к действующим на точку силам, образуя взаимно уравновешенную систему сил.
Принцип Даламбера для несвободной механической системыполучим, записывая
принцип Даламбера для каждой k-той точки и вводя реакции связей по аксиоме связей:
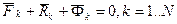 (4)
(4)
Здесь 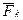 – равнодействующая задаваемых сил, приложенных к точке,
– равнодействующая задаваемых сил, приложенных к точке,
 – равнодействующая реакций связей, приложенных к точке,
– равнодействующая реакций связей, приложенных к точке,  – сила инерции точки.
– сила инерции точки.
На практике пользуются следствиями этих уравнений (принципа Даламбера).
Сложим все N уравнений: 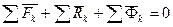 или
или
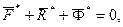 (5)
(5)
где 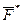 – главный вектор задаваемых сил, приложенных к точке,
– главный вектор задаваемых сил, приложенных к точке,
 – главный вектор реакций связей, приложенных к точке,
– главный вектор реакций связей, приложенных к точке, 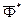 – главный вектор сил инерции точек системы.
– главный вектор сил инерции точек системы.
Следствие 1: Геометрическая сумма главных векторов задаваемых сил, реакций связи и сил инерции материальных точек равна нулю.
Умножим каждое из N уравнений, выражающее принцип Даламбера системы
на радиус-вектор, проведенный из центра O
 .
.
Теперь сложим все N уравнений:  или
или
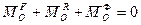 , (6)
, (6)
где 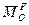 – главный момент задаваемых сил относительно центра O,
– главный момент задаваемых сил относительно центра O,
 – главный момент реакций связей относительно центра O,
– главный момент реакций связей относительно центра O,
 – главный момент сил инерции точек системы относительно центра O.
– главный момент сил инерции точек системы относительно центра O.
Следствие 2: Геометрическая сумма главных моментов задаваемых сил, реакций связи и сил инерции материальных точек относительно любого центра равна нулю.
Уравнения (5,6) называют обычно уравнениями метода кинетостатики.
Дата добавления: 2015-04-21; просмотров: 313; Мы поможем в написании вашей работы!; Нарушение авторских прав |