Потенциальное силовое поле и силовая функция МТ. Закон сохранения механической энергии

Среди сил, действующих на МТ, встречаются силы, зависящие только от положения этой МТ и времени.

Определение: Силовым полем называют часть пространства, в каждой точке которого на МТ действует определенная сила, зависящая от координат МТ и времени.

Определение:Силовое поле считается стационарным, если действующие силы не зависят от времени. Если же силы зависят от времени, то силовое поле называется нестационарным.

Предположим, что существует такая функция координат и времени U(х, у, z, t), частные производные которой по координатам равны проекции силы силового поля на соответствующие координатные оси, т. е.

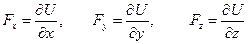. (1)

Определение:Функция U(х, у, z, t) называется силовой функцией данного силового поля, а само силовое поле называется потенциальным или консервативным, сила же потенциального силового поля называется потенциальной или консервативной.

Примерами консервативных сил являются сила тяжести, сила упругости и сила всемирного тяготения.

При наличии силовой функции выражение для элементарной работы силы потенциального стационарного силового поля примет вид:

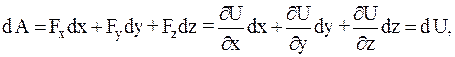
т.е.

dA = dU. (2)

Таким образом, элементарная работа силы в потенциальном стационарном силовом поле равна полному дифференциалу силовой функции.

Полная работа силы 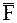на участке от точки В₀ до точки В можно выразить следующим образом:

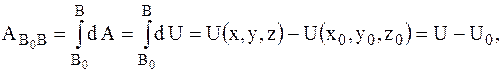т. е.

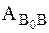= U – U₀, (3)

где

.

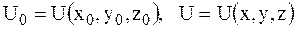Следовательно, полная работа силы на каком-либо перемещении МТ равна разности значений силовой функции в конечной и начальной точках перемещения и не зависит от формы траектории, по которой оно совершается, если силовая функция является однозначной.

Из (3) следует, что работа силы в потенциальном стационарном силовом поле по любому замкнутому пути равна нулю, если значение силовой функции в начальной и конечной точках перемещения одинаково, т. е. силовая функция является однозначной.

В случае потенциального силового поля наряду с силовой функцией можно ввести другую функцию, характеризующую запас энергии в данной точке поля – потенциальную энергию МТ в рассматриваемой точке силового поля.

Определение: Потенциальной энергией МТ – П в рассматриваемойточке В силового поля называют работу, которую совершают силы поля, действующие на МТ при перемещении ее из точки В в начальную точку В₀, т. е.

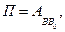
или

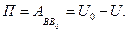(4)

На основании введенных соотношений имеем:

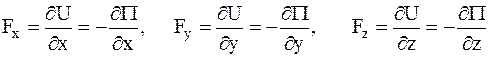. (5)

dA = dU = –dП, = U – U₀= П₀ – П. (6)

Так как силовая функция определяется с точностью до произвольной постоянной, то можно за счет выбора этой произвольной постоянной всегда достигнуть того, чтобы в точке В₀(x₀,y₀,z₀) силовая функция обратилась в ноль, т. е.

,

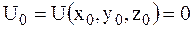и тогда получим:

П= –U. (7)

Для СМТ, состоящей из n МТ, в потенциальном стационарном силовом поле силовая функция имеет вид:

U=U(х₁, y₁, z₁, х₂, y₂, z₂, ... x_n, y_n, z_n).

Проекции силы, действующей на n-ю точку СМТ, можно представить в виде:

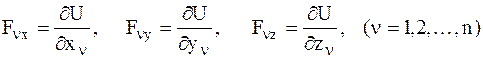. (8)

Сумма элементарных работ всех сил, действующих на СМТ, определяется по формуле:

или

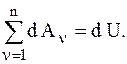(9)

Таким образом, сумма элементарных работ сил, действующих на СМТ, потенциального, стационарного силового поля равна полному дифференциалу от силовой функции.

Если вычислить сумму работ сил, действующих на СМТ в этом поле при перемещении СМТ из начального положения (I), в котором имеется силовая функция U₀, в положение (II), в котором есть силовая функция U, то:

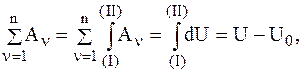
или

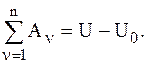
Определение: Потенциальной энергией СМТ – П в рассматриваемом положении называют сумму работ сил поля, действующих на СМТ, которую эти силы совершают при перемещении СМТ из рассматриваемого положения в начальное положение, т. е.

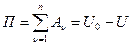, (10)

где U – значение силовой функции в рассматриваемом положении, U₀ – значение силовой функции в начальном положении.

Закон сохранения механической энергии МТ: При движении МТ в стационарном потенциальном силовом поле ее полная механическая энергия остается постоянной величиной.

Доказательство:

Теорема об изменении кинетической энергии МТ (соотношение (1.44))имеет следующий вид:

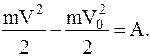
Если МТ движется в стационарном потенциальном силовом поле, то:

А = П_О – П.

Следовательно,

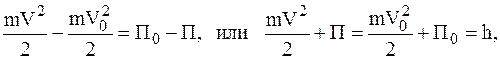
где h—постоянная величина.

Обозначая через Е полную механическую энергию МТ, состоящую из ее кинетической и потенциальной энергий, получаем:

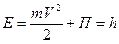. (11)

Закон сохранения механической энергии СМТ: полная механическая энергия при движении СМТ в стационарном потенциальном силовом поле внешних и внутренних сил является постоянной величиной

Доказательство:

Теорема об изменении кинетической энергии СМТ имеет вид:

T – T₀ = .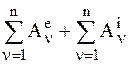

Если СМТ движется в стационарном потенциальном силовом поле, то:

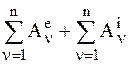= П₀ – П,

где П₀ и П – потенциальные энергии внутренних и внешних сил, действующих на СМТ в начальный и произвольный моменты времени. Следовательно,

Т – Т₀ = П₀ – П или T + П = T₀ + П₀ = h,

где h – постоянная величина.

Обозначая через Е полную механическую энергию СМТ, имеем:

E = T + П = h.

При движении МТ или СМТ в непотенциальном силовом поле, встречающемся в действительности, когда непотенциальность связана с действием сил сопротивления, механическая энергия изменяется, причем она всегда уменьшается на работу сил сопротивления.