Удар по вращающемуся телу. Определение реактивных ударных импульсов. Центр удара.

Рассмотрим АТТ массы М, закрепленное в точке О подпятником, а в точке В – подшипником (рис1).

Рис1

Пусть при этом ОВ= . Введем неизменно связанную с АТТ систему координат Охyz с осью Оz, которая направлена по оси вращения АТТ, и плоскостью Оyz, проведенной через центр масс С.

При действии на АТТ ударного импульса возникают реактивные ударные импульсы и . При этом реактивный ударный импульс в точке О может быть разложен на три составляющие , , , а в точке В – на две составляющие , .

Для определения этих пяти неизвестных воспользуемся теоремами о движении центра масс

(1)

и об изменении кинетического момента СМТ

(2)

при ударе в проекциях на оси декартовой системы координат.

Так как АТТ за время удара перемещается бесконечно мало, то векторы будут параллельны оси Оx и, следовательно,

где y_C – расстояние центра масс АТТ от оси вращения z , а w₀ и w – угловые скорости АТТ соответственно до и после удара.

Учитывая, что в данном случае , а 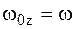, из формулы

получим:

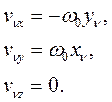
Проектируя соотношение

на оси декартовой системы координат Oxyz, получим проекции кинетического момента АТТ до удара на эти оси:

Аналогично для проекций кинетического момента АТТ после удара на оси декартовой системы координат получим:

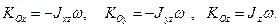
Подставив все эти значения в уравнения (1) и (2), имеем:

(3)

где – моменты ударного импульса относительно осей декартовой системы координат.

Из первых пяти уравнений (3) могут быть найдены пять неизвестных реактивных импульсов , , , , . Из шестого уравнения (3) определяется изменение угловой скорости АТТ (w – w₀), вращающегося вокруг неподвижной оси при ударе.

Найдем условия отсутствия ударных реактивных импульсов.

Для этого в первых пяти уравнениях (3) положим их равными нулю. Тогда уравнения (3) примут вид:

(4)

Из второго и третьего уравнений (4) следует, что для отсутствия ударных реактивных импульсов необходимо, чтобы приложенный ударный импульс был направлен параллельно оси Оx, то есть перпендикулярно плоскости yОz, которая проходит через ось вращения и центр масс АТТ (рис2).

Рис. 2

Так как систему координат можно выбрать произвольно, то выберем ее такой, чтобы ударный импульс лежал в координатной плоскости x₁O₁y₁ (точка О₁ расположена на оси вращения z). Тогда, направив согласно условиям параллельно оси O₁x₁, получим:

В результате четвертое и пятое из уравнений (4) дадут условия:

,

то есть ось вращения z для точки О₁ должна быть главной осью инерции.

Следовательно, для отсутствия ударных реактивных импульсов необходимо расположить ударный импульс в плоскости x₁O₁y₁, проходящей через точку О₁, для которой ось z является главной осью инерции.

Первое соотношение (4) примет вид:

(5)

Так как в рассматриваемом случае , где – кратчайшее расстояние линии действия ударного импульса от оси вращения z, то шестое соотношение формулы (4) примет вид:

. (6)

Из уравнений (5) и (6) найдем после исключения разности следующее соотношение:

(7)

Таким образом, уравнение (5) будет иметь место при любой численной величине ударного импульса , если линия действия этого импульса будет проходить через точку К, которая отстоит от оси вращения z на расстоянии y_К, определяемом формулой (7).

Условиями отсутствия ударных реактивных импульсов АТТ, вращающегося вокруг неподвижной оси, являются:

ударный импульс должен быть перпендикулярен плоскости, проходящей через ось вращения z и центр масс АТТ;

ударный импульс должен быть расположен в плоскости, перпендикулярной оси z и проходящей через точку О₁ АТТ, для которой ось z является главной осью инерции;

точка приложения К ударного импульса должна находиться от оси z на расстоянии, определяемом формулой (7) (точку К, через которую при этом проходит линия действия ударного импульса, не вызывающего ударных реакций в точках закрепления оси, называют центром удара).