Прямой центральный удар двух тел. Потеря кинетической энергии (теорема Карно) при прямом центральном ударе.

Удар двух АТТ, при котором общая нормаль к поверхностям АТТ в точке их соприкосновения проходит через их центры масс и скорости центров масс АТТ в начале удара направлены по этой общей нормали, называется прямым центральным ударом.

Рассмотрим прямой центральный удар двух поступательно движущихся АТТ с массами m₁ и m₂ . Обозначим скорости центров масс этих соударяющихся АТТ в начале удара через , а в конце удара – через .

Если второе АТТ находится впереди первого и , то первое АТТ нагонит второе и произойдет явление рассматриваемого удара (рис. 1).

Рис. 1

Задача о прямом центральном ударе двух АТТ состоит в том, чтобы, зная массы АТТ, скорости центров масс этих АТТ в начале удара и коэффициент восстановления, определить, во-первых, скорости центров масс АТТ в конце удара и, во-вторых, ударный импульс. Для решения этой задачи применим теорему об изменении количества движения СМТ при ударе к системе двух соударяющихся АТТ:

.

Действующими на эту систему ударными силами будут реакции в точке удара, являющиеся силами внутренними. Внешних ударных сил нет, поэтому сумма внешних ударных импульсов в данном случае равна нулю и теорема принимает вид:

или ,

т. е. количество движения СМТ в начале и конце удара одинаково.

Проектируя обе части этого векторного равенства на ось С₁x положительное направление на которой будем считать от С₁ к С₂, получим:

. (1)

В этом уравнении две неизвестных скорости . Чтобы определить эти неизвестные, надо найти второе уравнение, которое получим, если задать дополнительно коэффициент восстановления .

При соударении двух тел ударный импульс зависит не от абсолютного значения скорости каждого из АТТ, а от того, насколько скорость ударяющего АТТ превышает скорость ударяемого, т. е. от разности (относительной скорости) 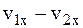. Снимая модуль, учтем, что , а :

,

Отсюда находим:

. (2)

Решая систему двух уравнений (1) и (2), получаем:

(3)

Для определения ударных импульсов , действующих на соударяющиеся АТТ при ударе, применим теорему об изменении количества движения СМТ только к одному из АТТ, например, к первому. Тогда внутренний ударный импульс в СМТ станет внешним ударным импульсом по отношению к первому АТТ и мы получим:

, ,

откуда на основании равенств (3) находим:

. (4)

Все эти уравнения получены в предположении, что поступательное движение АТТ до удара происходит в одном направлении.

Если второе АТТ до удара было неподвижно, то в формулах (3) и (4) следует положить , и тогда получим:

.

Если первое АТТ ударяется о неподвижную преграду (например, о стену), то следует принять в формулах (3) и . Поделив числитель и знаменатель соотношений (3) и (4) на и переходя к пределу при , найдем:

.

Эти формулы совпадают с теми, которые были получены ранее при изучении удара МТ о неподвижную поверхность.

Если удар не вполне упругий, то соударяющиеся АТТ не восстанавливают полностью своей формы в конце удара. Следовательно, часть кинетической энергии, которой обладали эти АТТ в начале удара, тратится на остающуюся деформацию их, а также на нагревание этих АТТ. Подсчитаем величину кинетической энергии, теряемой при прямом центральном ударе двух АТТ, полагая, что удар является не вполне упругим.

Предполагая, что соударяющиеся тела движутся поступательно, найдем кинетическую энергию СМТ, состоящую из двух АТТ, в начале и в конце рассматриваемого удара:

.

Следовательно, потеря кинетической энергии при ударе равна:

. (5)

Из уравнения (1) можно получить:

. (6)

Подставляя это значение в равенство (5) , получаем:

. (7)

Но из равенства (2) следует, что

,

из которого находим:

.

Подставляя это значение в равенство (7), получаем:

.

Используя равенство (6), полученную формулу представим в виде:

, (8)

где разности показывают, насколько уменьшилась при ударе скорость каждого из соударяющихся АТТ, а поэтому их называют потерянными при ударе скоростями.

Равенство (8) составляет содержание теоремы Карно: Кинетическая энергия, потерянная СМТ, при прямом центральном и не вполне упругом ударе двух АТТ, равна - й доле той кинетической энергии, которую имела бы СМТ, если бы ее АТТ двигались с потерянными скоростями.