Дифференциалы высших порядков.

Пусть у=ƒ(х) дифференцируемая функция, а ее аргумент х — независимая переменная. Тогда ее первый дифференциал dy=ƒ'(х)dx есть также функция х; можно найти дифференциал этой функции.

Дифференциал от дифференциала функции у=ƒ(х) называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается d²y или d²ƒ(х).

Итак, по определению d²y=d(dy). Найдем выражение второго дифференциала функции у=ƒ(х).

Так как dx=∆х не зависит от х, то при дифференцировании считаем dx постоянным:

d²y=d(dy)=d(f'(x)dx)=(ƒ'(х)dx)'•dx=f"(x)dx•dx=f"(x)(dx)² т. е.

d²y=ƒ"(х)dх². (24.5)

Здесь dx² обозначает (dx)².

Аналогично определяется и находится дифференциал третьего порядка

d³y=d(d²y)=d(ƒ"(х)dx²)≈f'(x)(dx)³.

И, вообще, дифференциал n-го порядка есть дифференциал от дифференциала (n-1)-го порядка: dⁿy=d(d^n-ly)=f⁽ⁿ⁾(x)(dx)ⁿ.

Отсюда находим, что 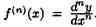, В частности, при n=1,2,3

соответственно получаем:

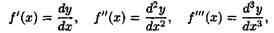
т. е. производную функции можно рассматривать как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.