
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоремы о средних значениях, (теоремы: Ферма,Ролля, Логранона, Коши).
По определению функция  достигает в точке
достигает в точке  локального максимума (минимума), если существует окрестность этой точки
локального максимума (минимума), если существует окрестность этой точки  , на которой выполняется неравенство
, на которой выполняется неравенство
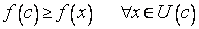 (1)
(1)
(соответственно  ) (1’)
) (1’)
Локальный максимум или минимум называется локальным экстремумом. Точка 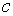 называется точкой локального экстремума.
называется точкой локального экстремума.
З а м е ч а н и е 1. Если функция  непрерывна на отрезке
непрерывна на отрезке 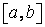 и достигает на нем максимума (минимума) в точке
и достигает на нем максимума (минимума) в точке  , то, очевидно,
, то, очевидно, 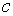 является в то же время точкой локального максимума (минимума)
является в то же время точкой локального максимума (минимума)  . Другое дело, если максимум (минимум)
. Другое дело, если максимум (минимум)  на
на 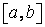 достигается одной из концевых точек отрезка. Такая точка не является точкой локального максимума (минимума)
достигается одной из концевых точек отрезка. Такая точка не является точкой локального максимума (минимума)  , потому что
, потому что  не определена в полной ее окрестности (справа от нее и слева).
не определена в полной ее окрестности (справа от нее и слева).
На рис. 49 изображен график функции 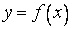 , непрерывной на
, непрерывной на 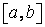 . Точки
. Точки  и
и  - это точки локального минимума
- это точки локального минимума  , а
, а 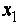 ,
, 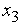 - точки локального максимума
- точки локального максимума  . Конечно, можно сказать, что
. Конечно, можно сказать, что 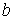 есть точка локального одностороннего максимума
есть точка локального одностороннего максимума  , а
, а  - локального одностороннего минимума
- локального одностороннего минимума  . Но
. Но  не есть точка локального минимума, а
не есть точка локального минимума, а 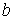 не есть точка локального максимума.
не есть точка локального максимума.
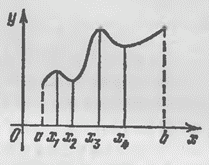
Рис. 49
Т е о р е м а 1 (Ферма). Если функция  имеет производную в точке
имеет производную в точке 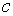 и достигает в этой точке локального экстремума, то
и достигает в этой точке локального экстремума, то  .
.
Д о к а з а т е л ь с т в о. Для определенности будем считать, что  имеет в точке
имеет в точке 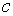 локальный максимум. По определению производной имеем
локальный максимум. По определению производной имеем
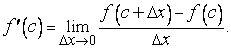
Так как у нас 
 , то для достаточно малых
, то для достаточно малых 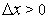
 ,
,
откуда в пределе при 
 . (2)
. (2)
Если же 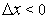 , то
, то
 ,
,
поэтому, переходя к пределу при  в этом неравенстве, получаем, что
в этом неравенстве, получаем, что
 . (3)
. (3)
Из соотношений (2) и (3) вытекает, что  .
.
Т е о р е м а 2 (Р о л л я).
Если функция 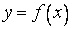 непрерывна на
непрерывна на 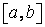 , дифференцируема на
, дифференцируема на 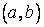 и
и 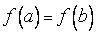 , то существует точка
, то существует точка 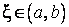 , такая, что
, такая, что  .
.
Д о к а з а т е л ь с т в о. Если  постоянна на
постоянна на 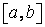 , то для всех
, то для всех 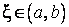 производная
производная  .
.
Будем теперь считать, что  непостоянна на
непостоянна на 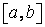 . Так как
. Так как  непрерывна на
непрерывна на 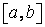 , то существует точка
, то существует точка  , в которой
, в которой  достигает максимума на
достигает максимума на 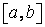 (см. § 3.5, теорема 2), и существует точка
(см. § 3.5, теорема 2), и существует точка 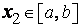 , в которой
, в которой  достигает минимума на
достигает минимума на 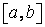 . Обе точки не могут быть концевыми точками отрезка
. Обе точки не могут быть концевыми точками отрезка 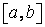 , потому что иначе
, потому что иначе
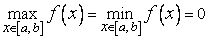
и  была бы постоянной на
была бы постоянной на 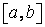 . Следовательно, одна из точек
. Следовательно, одна из точек 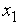 ,
, 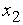 принадлежит к интервалу
принадлежит к интервалу 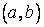 . Обозначим ее через
. Обозначим ее через  . В ней достигается локальный экстремум. Кроме того,
. В ней достигается локальный экстремум. Кроме того,  существует, потому что по условию
существует, потому что по условию  существует для всех
существует для всех 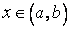 . Поэтому по теореме Ферма
. Поэтому по теореме Ферма  .
.
З а м е ч а н и е 2. Теорема Ролля сохраняет силу также для интервала 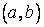 , лишь бы выполнялось соотношение
, лишь бы выполнялось соотношение
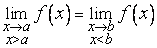 .
.
З а м е ч а н и е 3. Теорема Ролля теряет силу, если хотя бы в одной точке 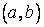
 не существует. Пример:
не существует. Пример:  на
на  . В теореме также нельзя заменить непрерывность на
. В теореме также нельзя заменить непрерывность на 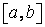 на непрерывность на
на непрерывность на 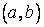 . Примером является функция
. Примером является функция
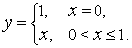
Точка  - точка разрыва.
- точка разрыва.
З а м е ч а н и е 4. Теорема Ролля имеет простой геометрический смысл. Если выполнены условия теоремы, то на графике (рис. 50) функции  существует точка
существует точка  , касательная в которой параллельна оси
, касательная в которой параллельна оси  .
.
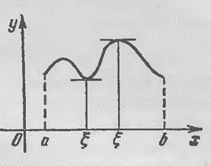
Рис. 50
Т е о р е м а 3 (Коши). Если функции  и
и 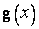 непрерывны на
непрерывны на 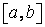 и дифференцируемы на
и дифференцируемы на 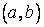 , и
, и  в
в 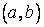 , то существует точка
, то существует точка 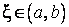 такая, что
такая, что
 . (4)
. (4)
Д о к а з а т е л ь с т в о. Отметим, что  , так как в противном случае, по теореме Ролля, нашлась бы точка
, так как в противном случае, по теореме Ролля, нашлась бы точка 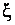 такая, что
такая, что 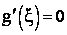 , чего быть не может по условию теоремы. Составим вспомогательную функцию
, чего быть не может по условию теоремы. Составим вспомогательную функцию
 .
.
В силу условия теоремы эта функция  непрерывна на
непрерывна на 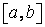 , дифференцируема на
, дифференцируема на 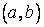 и
и 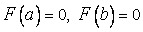 . Применяя теорему Ролля, получим, что существует точка
. Применяя теорему Ролля, получим, что существует точка 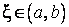 , в которой
, в которой 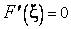 . Но
. Но
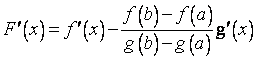 ,
,
поэтому, подставляя вместо  точку
точку 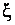 , получаем утверждение теоремы.
, получаем утверждение теоремы.
З а м е ч а н и е 5. В формуле (4) Коши, как нетрудно видеть, не обязательно считать  . Но тогда
. Но тогда 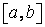 и
и 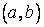 обозначают соответственно множества точек
обозначают соответственно множества точек  , для которых
, для которых  ,
,  .
.
Как следствие из теоремы Коши, при  получим теорему Лагранжа.
получим теорему Лагранжа.
Т е о р е м а 4 (о среднем Лагранжа). Пусть функция  непрерывна на отрезке
непрерывна на отрезке 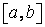 и имеет производную на интервале
и имеет производную на интервале 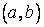 . Тогда существует на интервале
. Тогда существует на интервале 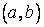 точка
точка 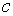 , для которой выполняется равенство
, для которой выполняется равенство
 . (5)
. (5)
Теорема Лагранжа имеет простой геометрический смысл, если записать ее в виде
 .
.
Левая часть этого равенства есть тангенс угла наклона к оси хорды, стягивающей точки  и
и 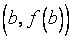 графика функции
графика функции 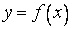 , а правая часть есть тангенс угла наклона касательной к графику в некоторой промежуточной точке с абсциссой
, а правая часть есть тангенс угла наклона касательной к графику в некоторой промежуточной точке с абсциссой  . Теорема Лагранжа утверждает, что если кривая (рис. 51) есть график непрерывной на
. Теорема Лагранжа утверждает, что если кривая (рис. 51) есть график непрерывной на 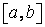 функции, имеющей производную на
функции, имеющей производную на 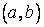 , то на этой кривой существует точка, соответствующая некоторой абсциссе
, то на этой кривой существует точка, соответствующая некоторой абсциссе 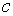
 такая, что касательная к кривой в этой точке параллельна хорде, стягивающей концы кривой
такая, что касательная к кривой в этой точке параллельна хорде, стягивающей концы кривой  и
и 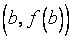 .
.
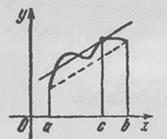
Рис. 51
Равенство (5) называется формулой (Лагранжа) конечных приращений. Промежуточное значение  удобно записывать в виде
удобно записывать в виде
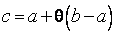 ,
,
где  есть некоторое число, удовлетворяющее неравенствам
есть некоторое число, удовлетворяющее неравенствам 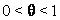 . Тогда формула Лагранжа примет вид
. Тогда формула Лагранжа примет вид
 . (6)
. (6)
Она верна, очевидно, не только для  , но и для
, но и для 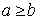 .
.
Т е о р е м а 5. Функция, непрерывная на отрезке 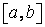 , где
, где  , и имеющая неотрицательную (положительную) производную на интервале
, и имеющая неотрицательную (положительную) производную на интервале 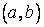 , не убывает (строго возрастает) на
, не убывает (строго возрастает) на 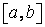 .
.
Действительно, пусть  , тогда на отрезке
, тогда на отрезке  выполняются условия теоремы Лагранжа. Поэтому найдется на интервале
выполняются условия теоремы Лагранжа. Поэтому найдется на интервале 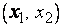 точка
точка 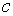 , для которой
, для которой
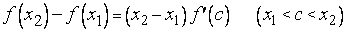 .
.
Если по условию  на
на 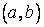 , то
, то  и
и
 ; (7)
; (7)
если же  на
на 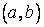 , то
, то  и
и
 . (8)
. (8)
Так как неравенства (7) и (8) имеют место, каковы бы ни были  , где
, где  , то в первом случае
, то в первом случае  не убывает, а во втором
не убывает, а во втором  строго возрастает на отрезке
строго возрастает на отрезке 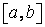 .
.
Дата добавления: 2015-04-21; просмотров: 1459; Мы поможем в написании вашей работы!; Нарушение авторских прав |