Основные правила дифференцирования. Сумма.

Выведем несколько правил вычисления производных, В этом пункте значения функций u и v и их производных в точке х₀ обозначаются для краткости так: u(х₀) = u, v(х₀) = v, u'(х₀) = u', v'(х₀)=v`. Если функции u и v дифференцируемы в точке х₀, то их сумма дифференцируема в этой точке и

(u+v)' = u' + v'.

Коротко говорят: производная суммы равна сумме производных.

1) Для доказательства вычислим сначала приращение суммы функций в рассматриваемой точке: Δ(u+v) = u (х₀+Δx)+ v(х₀+Δx) – (u(х₀)+v(х₀)) = (u(х₀+Δx)-u(х₀)) + (v(х₀+Δx)-v(х₀)) = Δu + Δv

2)

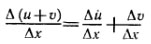
3) Функции u и v дифференцируемы в точке х₀, т. е. при Δх→0

Тогда

при Δх→0 (см. правило 3, а) предельного перехода), т. е. (u+v)' = u'+v’

Лемма. Если функция f дифференцируема в точке х₀, то она непрерывна в этой точке: Δf→0 при Δx→0, т. е.

f(х₀ + Δх)→f (х₀) при Δx→0

.

Действительно,

при Δх→0, так как

Итак, Δf→0 при Δx→0, т. е. для дифференцируемых функций f (х₀ + Δx)→f (х₀) при Δх→0.