Предел функции в точке. Графическая интерпретация предела.

Пусть функция у=ƒ (х) определена в некоторой окрестности точки хо, кроме, быть может, самой точки хо.

Сформулируем два, эквивалентных между собой, определения предела функции в точке.

Определение 1 (на «языке последовательностей», или по Гейне).

Число А называется пределом функции у=ƒ(х) в топке x0 (или при х® хо), если для любой последовательности допустимых значений аргумента xn, n є N (xn¹x0), сходящейся к хо последовательность соответствующих значений функции ƒ(хn), n є N, сходится к числу А

В этом случае пишут

или ƒ(х)—>А при х→хо. Геометрический смысл предела функции: означает, что для всех точек х, достаточно близких к точке хо, соответствующие значения функции как угодно мало отличаются от числа А.

Определение 2 (на «языке ε», или по Коши).

Число А называется пределом функции в точке хо (или при х→хо), если для любого положительного ε найдется такое положительное число δ, что для все х¹хо, удовлетворяющих неравенству |х-хо|<δ, выполняется неравенство |ƒ(х)-А|<ε.

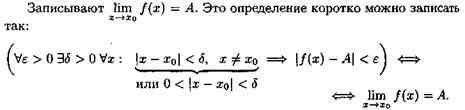
Геометрический смысл предела функции:

если для любой ε-окрестности точки А найдется такая δ-окрестность точки хо, что для всех х¹хо из етой δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε, ограниченной прямыми у=А+ ε , у=А-ε. Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε).

Предел функции при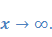

Пусть функция у=ƒ(х) определена в промежутке (-∞;∞). Число А называется пределом функции ƒ(х) при х→∞, если для любого положительного числа ε существует такое число М=М()>0, что при всех х, удовлетворяющих неравенству |х|>М выполняется неравенство |ƒ(х)-А|<ε. Коротко это определение можно записать так:

Геометрический смысл этого определения таков: для "ε>0 $ М>0, что при х є(-∞; -М) или х є(М; +∞) соответствующие значения функции ƒ(х) попадают в ε-окрестность точки А, т. е. точки графика лежат в полосе шириной 2ε, ограниченной прямыми у=А+ε и у=А-ε (см. рис. 112).