Понятие функции. Числовые функции. Способы задания функции.

Функция - это зависимость одной величины от другой. Если элементами множеств X и Y явл. действительные числа, то функцию f наз. числовой функцией. Определение способа задания:

-аналитически (y=kx+b)

-графический (график)

-таблично

-алгоритмически (с помощью ЭВМ)

Основные характеристики функции:

a) Четность и нечетность;

b) Возрастание убывание;

c) Ограниченность;

d) Периодичность.

Функция y=f(x), определенная на множестве D наз. четной, если выполняется условие нечетной, если выполняется условие 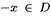и График четной функции симметричен относительно оси O_Y, а нечетной - относительно начала координат. Если для любых значений х₁,х₂ принадлежащих D₁ аргументов из неравенства х₁<х₂ вытекает неравенство f(x₁)<f(x₂), то функция наз. возрастающей на множестве D_1. f(x₁)>f(x₂), то функция наз. убывающей на множестве D_1. Функцию y=f(x), определенную на множестве D наз. ограниченной на этом множестве, если сущ. такое число M>0, что для всех выполняется неравенство 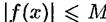. Функция y=f(x), определенная на множестве D наз. периодической на этом множестве, если сущ. такое число T>0, что при каждом значение