Исследование формы параболы по уравнению.

Исследование форм параболы по ее уравнению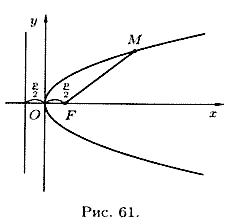

1. В уравнении (11.13) переменная у входит в четной степени, значит, парабола симметрична относительно оси Ох; ось Ох является осью сим­метрии параболы.

2. Так как ρ > 0, то из (11.13) следует, что 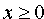. Следовательно, парабола рас­положена справа от оси Оу.

3. При имеем у = 0. Следователь­но, парабола проходит через начало коор­динат.

4. При неограниченном возрастании x модуль у также неограниченно возраста­ет. Парабола имеет вид (форму), изображенный на рисунке 61. Точ­ка О(0; 0) называется вершиной параболы, отрезок FM = r называется фокальным радиусом точки М.

Уравнения 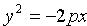, , 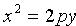(p>0) также определяют параболы, они изображены на рисунке 62

Нетрудно показать, что график квадратного трехчлена , где 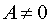, B и С любые действительные числа, представляет собой параболу в смысле приведенного выше ее определения.