
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие о линейной зависимости системы функций.
Функции f1 f2 fn наз. линейно-зависимыми, если сущ. Такие постоянные с1 с2… сn не все одновременно =0,что имеет место равенство: с1f1+c2f2+…+cnfn=0, если равенство выполняется, тогда когда все они равны нулю то f1 f2 fn наз. линейно-независимыми.
Понятие линейной зависимости и независимости относится к функциям, строкам и столбцам матрицы к системе векторов и к другим объектам.
Связь между рангом матрицы и числом линейно независимых строк (столбцов) Базисный минор.
Если ранг матрицы r(A)=r, то сущ. R линейно-независимых строк,от которых зависят все остальные.
Следствие:1.если r(A)=r, то сущ. R линейно-независимых столбцов, от которых зависят все остальные столбцы.2.максим.число лин.-независ. строк в матрице = максим.числу лин.-незав. столбцов матрицы и = рангу матрицы.
Базисным минором в матрице наз. отличный от нуля ее минор,порядок которого раевн рангу матрицы. Он может быть не один.
Матричная запись системы линейных уравнений. Основные понятия и определения.
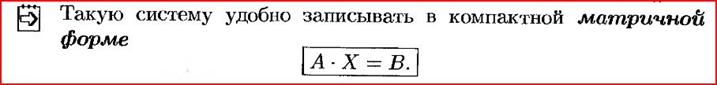






Дата добавления: 2015-04-21; просмотров: 254; Мы поможем в написании вашей работы!; Нарушение авторских прав |