Обратная матрица. Теорема существования обратной матрицы. Теорема о единственности.

ТЕОРЕМА

Всякая невырожденная матрица имеет обратную.

Единственность обратной матрицы докажем от противного. Пусть кроме существует еще одна обратная матрица такая что АВ = Е. Умножая обе части этого равенства на , получаем . Отсюда следует что , что противоречит предположению . Следовательно, обратная матрица единственная.

Ранг Матрицы и его вычисление. (два метода вычисления)

Ранг матрицы – это наибольший из порядков миноров данной матрицы, отличных от нуля. Если все миноры равны 0 то и матрица равна 0.Обозначается r(А).

Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы их может быть несколько.

ВЫЧИСЛЕНИЕ РАНГА МАТРИЦЫ

Способ 1

Метод элементарных преобразований

Дана матрица:

Выполняя элементарные преобразования получаем: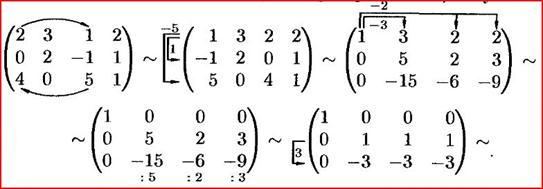

То есть:

Таким образом, ранг матрицы = 2.

Способ 2

Метод окаймляющих миноров

Дана матрица:

Все миноры 3-го порядка =0. Есть минор 2-го порядка, отличный от нуля Значит ранг матрицы равен 2.

СВОЙСТВА РАНГА МАТРИЦЫ

1. При транспонировании матрицы ее ранг не меняется.

2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.

3. Ранг матрицы не изменится при элементарных преобразованиях матрицы.

Ранг канонической матрицы равен числу единиц на главной диагонали.