Линейные операции над матрицами. Умножение матриц. Свойства.

Линейная и векторная алгебра. Аналитическая геометрия.

Матрицы. Основные определения.

Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длинны или n столбцов одинаковой длинны

Матрицы равны между собой, если равны все соответствующие элементы этих матриц.

Матрица называется квадратной если у нее число строк = числу столбов. Матрицу размера n x n называют матрицей n-го порядка.

Квадратная матрица ,у которой все элементы, кроме главной диагонали, равны 0, называется диагональной.

Диагональная матрица, у которой каждый элем главной диагонали =1, называется единичной и обозначается Е.

Квадратная матрица называется треугольной, если все элементы по одну из сторон главной диагонали =0.

Матрица, все элементы которой =0, называется нулевой и обозначается О.

Матрица, содержащая один столбец или строку, называется вектором.

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной к данной. Обозначается .

Линейные операции над матрицами. Умножение матриц. Свойства.

СЛОЖЕНИЕ

Сложение и вычитание можно сделать только с матрицами одинаковых размеров.

УМНОЖЕНИЕ НА ЧИСЛО

СВОЙСТВА СЛОЖЕНИЯ МАТРИЦ И УМНОЖЕНИЯ МАТРИЦЫ НА ЧИСЛО.

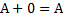
ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ МАТРИЦ:

- Перестановка местами двух параллельных рядов матрицы

- Умножение всех элементов ряда матрицы на число отличное от нуля

- Прибавление ко всем элементам ряда соответствующих элементов другого ряда, умноженных на одно и тоже число.

ПРОИЗВЕДЕНИЕ МАТРИЦ

Операция умножения двух матриц вводится только в том случае, когда число столбцов первой матрицы равно числу строк второй матрицы.

Если матрицы А и В квадратные то произведение АхВ и ВхА всегда существуют.

Матрицы А и В называются перестановочными, если АВ=ВА

СВОЙСТВА УМНОЖЕНИЯ МАТРИЦ

ЕСЛИ, КОНЕЧНО, НАПИСАННЫЕ СУММЫ И ПРОИЗВЕДЕНИЯ ИМЕЮТ СМЫСЛ

ДЛЯ ОПЕРАЦИИ ТРАНСПОНИРОВАНИЯ ВЕРНЫ СВОЙСТВА: