Замечание 14.1 С математической точки зрения поверхность (14.10) лучше определять с помощью уравнения

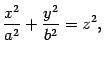
(14.11)

так как в нем меньше параметров, но при этом, во-первых, теряется аналогия с уравнениями предыдущих поверхностей, а во-вторых, если считать, что величины 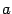, , 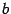, , 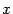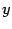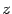имеют размерность длины, то в уравнении (14.11) размерности правой и левой части не согласуются.

Для краткости в дальнейшем конус второго порядка будем называть просто конус. Исследуем форму конуса. Так же, как эллипсоид и гиперболоиды, он имеет три плоскости симметрии, три оси симметрии и центр симметрии. Ими являются соответственно координатные плоскости, координатные оси и начало координат.

Для построения конуса найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью 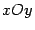. На этой плоскости , поэтому

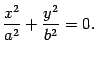
Координаты только одной точки плоскости 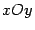могут удовлетворять данному уравнению, а именно, начала координат. Найдем линию пересечения с плоскостью . На этой плоскости 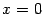, поэтому

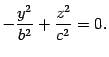
Это уравнение пары прямых 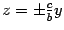на плоскости . Построим эти прямые (рис. 14.16). Сечение плоскостью 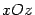также является парой прямых с уравнением 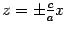. Нарисуем и эти прямые (рис. 14.16).

Рис.14.16.Сечения конуса координатными плоскостями

Найдем линии пересечения поверхности с плоскостями 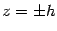, 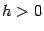. Уравнения этих линий

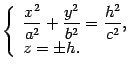
Первое уравнение преобразуем к виду

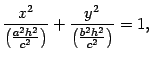
то есть к виду

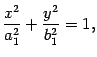
(14.12)

где , 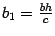. Уравнение (14.12) является уравнением эллипса. Нарисуем полученные сечения (рис. 14.17).

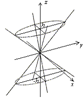
Рис.14.17.Изображение конуса с помощью сечений

Точка пересечения конуса с плоскостью 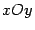называется вершиной конуса.

Если в уравнении (14.10) , то сечения конуса плоскостями параллельными плоскости 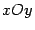являются окружностями. В этом случае поверхность называется прямым круговым конусом и может быть получена вращением прямой, лежащей в плоскости , вокруг оси . Именно с таким конусом мы имеем дело в школьном курсе математики.

Канонические уравнения поверхностей второго порядка:

g) Эллипсоид;

h) Однополостный гиперболоид;

i) Дпухполостный гиперболоид;

j) Элиптический параболоид;

k) Гиперболический параболоид;

l) Конус второго порядка.

Для любой алгебраической поверхности второго порядка существует прямоугольная система координат Oxyz, в которой уравнение этой поверхности принимает один из следующих семнадцати канонических видов:

1.		уравнение эллипсоида;
2.		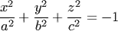уравнение мнимого эллипсоида;
3.		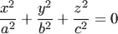уравнение мнимого конуса;
4.		уравнение однополостного гиперболоида;
5.		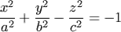уравнение двуполостного гиперболоида;
6.		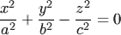уравнение конуса;
7.		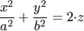уравнение эллиптического параболоида;
8.		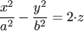уравнение гиперболического параболоида;
9.		уравнение эллиптического цилиндра;
10.		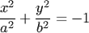уравнение мнимого эллиптического цилиндра;	{TEXT10}
11.		уравнение пары мнимых пересекающихся плоскостей;	{TEXT11}
12.		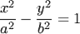уравнение гиперболического цилиндра;	{TEXT12}
13.		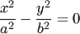уравнение пары пересекающихся плоскостей;	{TEXT13}
14.		уравнение параболического цилиндра;	{TEXT14}
15.		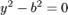уравнение пары параллельных плоскостей;	{TEXT15}
16.		уравнение мнимых пары параллельных плоскостей;	{TEXT16}
17.		уравнение пары совпадающих плоскостей.	{TEXT17}

В этих уравнениях 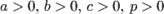, причем 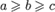в уравнениях 1,2; в уравнениях 3,4,5,6,7,9,10.