Устойчивость управленческих решений.

Точность – соотв-ие расчетной величины функционала ее фактической величине.

Стационарность ПП (оценка стационарности) – хар-ка, отражающая постоянство во времени планируемых показателей – устойчивость. Выбор рационального варианта организации работ по подготовке и реал-ции проекта осущ-ся в 2 этапа:

1) форм-ся множество допустимых вариантов; 2) организуется поиск рационал. (оптимал.) варианта по одному из выбранных критериев (по устойчивости). Устойчивость (достоверность) решения в процессе упр-ния ИП зависит от:

- достоверность (точность, степень погрешности) исходных данных; - качество моделей и вычислит. процедур (алгоритмов).

Неопр-ть в принятии решений обусловлена недостаточной надежностью и кол-вом инф-ции, на основе которой орган принятия решения осущ-ет выбор решения.

Энтропия – неопр-ть, связанная с кол-вом элементов и связей в системе. Любое организационное изменение – попытка уменьшения степени разнообразия производ. системы (энтропии).

Мера разнообразия независимого объекта A с конечным множ-вом возможных состояний и с соотв-ми вероятностями этих состояний 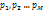: 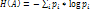, где Н(А) – энтропия объекта А; i – состояние объекта А (i = 1 … N); 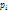– вероятность наступления состояния i.

Если исходить из принципиальной возм-ти расчета энтропии, то эта хар-ка становится основным оценочным пок-лем организационности проекта. Процесс упр-ния распадается на периоды, для которых формируют модели. Попытка снизить неопр-ть, которая создается внешней средой – процесс прогнозирования.

Мера устойчивости зависит от периода планирования (горизонта план-ния) → принцип. возм-ть обоснования горизонтов план-ния как величины соотв-ей разумному уровню устойчивости.

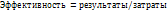
Билет №20. Задача «Время-стоимость»

В решении задач маркетинга, менеджмента необходимо учитывать, контролировать и прогнозировать множество факторов – продолжительность работы; стоимость изготовления; количество исполнителей и т.д. Все факторы зависят друг от друга. Иногда эту зависимость определить трудно, но она все равно есть.

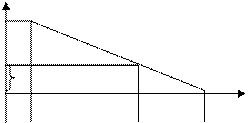
Зависимость между длительностью работы и ее стоимостью с некоторой долей условности можно представить в виде аппроксимирующей прямой, имеющей линейную зависимость (рис)

C(ij)

C_max

C_изм

∆С

С_min

t_min t_изм t_max t(ij)

Рис. График «время-стоимость» работы (ij)

Чем более мы стремимся сократить время работы, тем дороже она нам обходится. Для каждого вида работ можно определить коэффициент возрастания затрат на единицу времени:

t_max(ij) – t_min(ij)

алгоритм оптимизации сетевой модели по критерию «стоимость»:

Дано: Сетевая модель. По каждой работе (ij) дается возможный диапазон длительности работы t_min(ij), t_max(ij), минимальная стоимость работы C_min(ij),коэффициент S(ij). Необходимо найти зависимость Ткр между и суммарными затратами, ставя задачу обеспечить минимум возрастания затрат при уменьшении Ткр.

Алгоритм заключается в следующем:

1. Найти критический путь, его длину Ткр.

С = ∑С(ij)

Lкр = (i₀, i₁,…,i_n) из предположения t(ij) = t_max(ij)

2. На этом пути найти работу (kℓ) Є Lкр, у которой S(kℓ) будет иметь наименьшее значение.

3. Для выбранной работы найти величину ∆t(kℓ) = t_max(kℓ) - t_min(kℓ)

4. Определить ∆С(kℓ) = S(kℓ)*∆t(kℓ)

5. Следовательно, при уменьшении Ткр на величину ∆t(kℓ) стоимость всех работ увеличивается на величину ∆С(kℓ)

С^* = С_пред. + ∆С(kℓ)

6. Рассчитать сетевую модель с учетом измененной продолжительности работы (kℓ).

7. Возвратиться к п.1. В результате реализации данного алгоритма получается график зависимости С от Ткр. По этому графику легко координировать отношения между инвестором и производителем.