Ячейка Вигнера–Зейтца

Решетки Бравэ

Каждую кристаллическую структуру можно охарактеризовать определенным набором элементарных трансляций. В зависимости от отношения значений и взаимной ориентации основных трансляций a, b, c получаются решетки, отличающиеся друг от друга по своей симметрии. Бравэ доказал, что существует всего 14 типов решеток, отличающихся по своей симметрии. Они названы решетками Бравэ. Среди этих 14 решеток 7 являются примитивными ибазисными. Распределение 14 решеток Бравэ по 7 сингониям показано в табл. 1.2

Ячейка Вигнера–Зейтца

Вигнером и Зейтцем был предложен способ построения таких примитивных ячеек, которые обладали бы полной симметрией решетки Бравэ. Этот способ состоит в том, что произвольно выбранный узел решетки Бравэ соединяют прямыми линиями с ближайшими эквивалентными узлами; затем проводят плоскости, перпендикулярные этим прямым и проходящие через их середину (рис. 1.11 а). В результате получают замкнутую область пространства с центром в выбранном узле, все точки которого лежат ближе к нему, чем к любому другому узлу решетки. Эта область носит название ячейки Вигнера–Зейтца. Она примитивна, поскольку только атом в центре принадлежит ей. Объем ее равен объему элементарной ячейки, построенной на кратчайших трансляциях решетки.

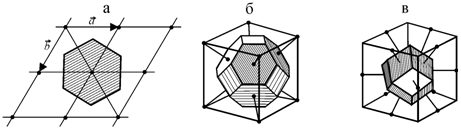
Ячейка Вигнера-Зейтца для примитивной кубической решетки имеет форму куба. Для объемноцентрированной кубической (ОЦК) решетки выберем в качестве исходного узла центральный узел куба. Восемь перпендикулярных плоскостей, проведенных через середины отрезков, соединяющих исходный узел с узлами, находящимися в вершинах куба, образуют правильный восьмигранник (октаэдр). Шесть перпендикулярных плоскостей, проведенных через середины отрезков, соединяющих исходный узел с узлами, находящимися в центре соседних кубов, отсекут шесть вершин октаэдра, образуя четырнадцатигранник. Восемь его граней - правильные шестиугольники, а шесть граней – квадраты (рис. 1.11 б). Аналогично можно построить ячейку Вигнера-Зейтца для гранецентрированной кубической (ГЦК) решетки (рис. 1.11 в). Ячейки Вигнера-Зейтца будут в дальнейшем необходимы при рассмотрении тепловых и электрических свойств кристаллических твердых тел.

Рис. 1.11. Ячейка Вигнера−Зейтца: а – двумерный случай (заштрихованная область), б – для объемноцентрированной кубической ячейки, в – для гранецентрированной кубической ячейки