Определение

Чтобы вычислять плотность состояний энергии для частицы, мы сначала вычислим плотность состояний в обратном пространстве (импульсное или k-пространство). Расстояние между состояниями задано граничными условиями. Для свободных электронов и фотонов в пределах ящика размера L, и для электронов в кристаллической решётке с размером решетки L используем периодические граничные условия Борна — фон Кармана. Используя волновую функцию свободной частицы получаем

где n — любое целое число, а — расстояние между состояниями с различными k.

Полное количество k-состояний, доступных для частицы - объем k-пространства доступного для неё, разделенного на объём k-пространства, занимаемого одним состоянием. Доступный объем - просто интеграл от к . Объём k-пространства для одного состояния в n-мерном случае запишется в виде

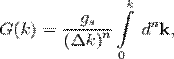
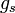— вырождение уровня (обычно это спиновое вырождение равное 2). Это выражение нужно продифференцировать, чтобы найти плотность состояний в k-пространстве: . Чтобы найти плотность состояний по энергии нужно знать закон дисперсии для частицы, то есть выразить k и dk в выражении g(k)dk в терминах E и dE. Например для свободного электрона: ,

С более общим определением связано соотношение

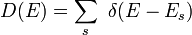
где индекс s соответствует некоторому состоянию дискретного или непрерывного спектра, а — дельта-функция Дирака. При переходе от суммирования к интегрированию следут использовать правило

где — постоянная Планка.

В следующей таблице представлены плотность состояний для электронов с параболическим законом дисперсии

	Доступный объём	Объём для одного состояния	Плотность состояний
33D
22D
11D
00D

где l — индекс подзоны размерного квантования. Здесь рассмотрен не чистый случай, а когда квантование по одному или нескольким направлениям связано с некоторым ограничивающим потенциалом.

27) Уравнения движения электронов и дырок во внешних полях.

дикулярной магнитному полю. Угловая скорость этого вращения равна ω_с.

28) Искривление энергетических зон в электрическом поле.

29) Связь зонной структуры с оптическими свойст­вами полупроводника.

Поглощение света полупроводниками обусловлено переходами между энергетическими состояниями зонной структуры. Учитывая принцип запрета Паули, электроны могут переходить только из заполненного энергетического уровня на незаполненный. В собственном полупроводнике все состояния валентной зоны заполнены, а все состояния зоны проводимости незаполненные, поэтому переходы возможны лишь из валентной зоны в зону проводимости. Для осуществления такого перехода электрон должен получить от света энергию, превышающую ширину запрещённой зоны. Фотоны с меньшей энергией не вызывают переходов между электронными состояниями полупроводника, поэтому такие полупроводники прозрачны в области частот , где — ширина запрещённой зоны, — постоянная Планка. Эта частота определяет фундаментальный край поглощения для полупроводника. Для полупроводников, которые зачастую применяются в электронике (кремний, германий, арсенид галлия) она лежит в инфракрасной области спектра.

Дополнительные ограничения на поглощение света полупроводников накладывают правила отбора, в частности закон сохранения импульса. Закон сохранения импульса требует, чтобы квазиимпульс конечного состояния отличался от квазиимпульса начального состояния на величину импульса поглощённого фотона. Волновое число фотона 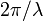, где — длина волны, очень мало по сравнению с волновым вектором обратной решётки полупроводника, или, что то же самое, длина волны фотона в видимой области намного больше характерного межатомного расстояния в полупроводнике, что приводит к требованию того, чтобы квазиимпульс конечного состояния при электронном переходе практически равнялся квазиимпульсу начального состояния. При частотах, близких к фундаментальному краю поглощения, это возможно только для прямозонных полупроводников. Оптические переходы в полупроводниках, при которых импульс электрона почти не меняется называются прямыми или вертикальными. Импульс конечного состояния может значительно отличаться от импульса начального состояния, если в процессе поглощения фотона участвует ещё одна, третья частица, например, фонон. Такие переходы тоже возможны, хотя и менее вероятны. Они называются непрямыми переходами.

Таким образом, прямозонные полупроводники, такие как арсенид галлия, начинают сильно поглощать свет, когда энергия кванта превышает ширину запрещённой зоны. Такие полупроводники очень удобны для использования в оптоэлектронике.

Непрямозонные полупроводники, например, кремний, поглощают в области частот света с энергией кванта чуть больше ширины запрещённой зоны значительно слабее, только благодаря непрямым переходам, интенсивность которых зависит от присутствия фононов, и следовательно, от температуры. Граничная частота прямых переходов кремния больше 3 эВ, то есть лежит в ультрафиолетовой области спектра.

При переходе электрона из валентной зоны в зону проводимости в полупроводнике возникают свободные носители заряда, а следовательно фотопроводимость.

При частотах ниже края фундаментального поглощения также возможно поглощение света, которое связано с возбуждением экситонов, электронными переходами между уровнями примесей и разрешенными зонами, а также с поглощением света на колебаниях решётки и свободных носителях. Экситонные зоны расположены в полупроводнике несколько ниже дна зоны проводимости благодаря энергии связи экситона. Экситонные спектры поглощения имеют водородоподобную структуру энергетических уровней. Аналогичным образом примеси, акцепторы или доноры, создают акцепторные или донорные уровни, лежащие в запрещённой зоне. Они значительно модифицируют спектр поглощения легированного полупроводника. Если при непрямозонном переходе одновременно с квантом света поглощается фонон, то энергия поглощенного светового кванта может быть меньше на величину энергии фонона, что приводит к поглощению на частотах несколько ниже по энергии от фундаментального края поглощения.

30) Уровни энергии, создаваемые примесными центрами в полупро­водниках.

31) Доноры и акцепторы.

Рассмотрим сначала поведение примесных атомов. Наиболее простой и ясный случай мы имеем для примесей элементов III и V групп периодической системы в полупроводниках подгруппы IVB (кремний, германий). Такие примеси образуют твердый раствор замещения. На это, в частности, указывают очень малые значения их коэффициентов диффузии,

Атом любого элемента V группы имеет 5 валентных электронов, и, соответственно, его ионный остаток несет положительный за­ряд +5е. Однако для образования тетраэдрических валентных связей в решетке типа алмаза необходимо только 4 электрона, Поэтому при замене атома основной решетки на атом примеси мы получим один «лишний» электрон. Последний будет двигаться в поле ионного остатка и остальных валентных электронов, т. е. в поле эффективного заряда +е, образуя систему, подобную атому водо­рода (рис, 2.18, а). Этот дополнительный электрон может быть отщеплен от своего узла решетки под действием тепловых колеба­ний, освещения и т. п., и тогда он превратится в электрон проводи­мости. При этом образования свободной положительной дырки (как в случае разрыва связей в собственном полупроводнике) не будет. Из сказанного видно, что примеси элементов V группы в по­лупроводниках с решеткой алмаза являются донорами,

В случае узельного атома элемента III группы (В, А1 и др.) имеется всего 3 валентных электрона, т. е. не хватает одного элек­трона для завершения валентных связей. Этот недостающий элек­трон может быть заимствован из числа соседних электронов связи. При этом образуется вакантное место среди соседних электронов связи, или положительная дырка, которая окажется в поле заряда ионного остатка (+3е) и четырех электронов связи (—4е), т. е. в поле эффективного заряда —е (рис. 2.18, б). Так как в образовавшуюся вакансию могут переходить другие электроны связи, то дырка будет двигаться вокруг примесного центра, и мы опять получим водородоподобную систему, но только с неподвижным отрицатель­ным зарядом и подвижным положительным зарядом.

Под влиянием теплового движения, освещения и иных внешних воздействий в образовавшуюся вакансию могут быть заброшены более удаленные электроны связи. Тогда вместо дырки, связанной с данным примесным центром, появится дырка в другом месте, и эта дырка, вследствие последовательного заброса в нее других электронов связи, будет перемещаться в кристалле. Этот процесс аналогичен отрыву связанного электрона от донора V группы и может быть назван освобождением связанной дырки и переводом ее в свободное состояние. Образования же электрона проводимости при этом не происходит. Из сказанного видно, что атомы элементов III группы в решетке типа алмаза являются акцепторами.

Примесные центры, которые могут отдавать или, соответственно, принимать только один электрон и, следовательно, находиться только в двух различных зарядных состояниях, мы будем в даль­нейшем называть простыми. Из сказанного выше следует, что простой донор есть такой примесный центр, с которым при завершенных валентных связях связан один элект­рон. И, аналогично, простой акцеп­тор есть такой примесный центр, с которым при завершенных валентных связях связана одна дырка.

Простые доноры можно охаракте­ризовать заданием наинизшего уровня энергии E_t неотщепленного электрона (основное состояние). Аналогично, для простого акцептора можно за­дать один уровень энергии захваченного электрона. Такие уровни, однако, в отличие от уровней элек­тронов проводимости, являются локальными, так как электроны, их занимающие, расположены в непосредственной близости от при­месных центров (рис. 2.19). Энергия ионизации донора J_d на этой диаграмме равна (Е_с — E_t). Аналогично, энергия, необходимая для заброса электрона из валентной зоны на акцептор (или, другими словами, энергия отрыва связанной дырки от акцептора J_а), рав­на (E_t — E_v).

Рис. 2.19. Уровни энергии элек­тронов в кристалле при нали­чии простых доноров или ак­цепторов.

Энергию ионизации примесных атомов в кристалле можно экспе­риментально определить либо из температурной зависимости посто­янной Холла («термическая» энергия ионизации), либо из спектраль­ных зависимостей коэффициента поглощения света и фотопроводи­мости («оптическая» энергия ионизации). Значения энергии ионизации атомов III и V групп в германии и кремнии, определенные из оптических измерений при гелиевых температурах, приведены в таблице 2.1. Энергии ионизации в гер­мании мало отличаются друг от друга и близки к 0,01 эВ.

Вследствие малой энергии ионизации атомы этих элементов в германии практически полностью ионизованы, уже, начиная с температур ~10К и выше. Энергии ионизации этих элементов в кремнии, особенно акцепто­ров III группы, отличаются значительно сильнее. Однако и здесь (за исключением In) энергия их ионизации невелика, и поэтому при температурах, близких к комнатным (и выше), атомы этих элементов тоже ионизованы почти полностью. С другой стороны, растворимость большинства элементов III и V групп (кроме Bi и Тl) в германии и кремнии очень велика (например, для In, Ga, Р в германии она приближается к 10²¹ атомов/см³). Поэт/эму, вводя элементы III и V групп в германий и кремний, можно в широких пределах менять концентрацию электронов и дырок и, соответ­ственно, электропроводность. Подобные примеси, создающие мелкие уровни энергии и способные входить в решетку полупроводника в больших концентрациях, мы в дальнейшем будем называть леги­рующими примесями.

На рис. 2.20 в качестве примера приведены примесные уровни энергии в германии, который изучен наиболее подробно. Остано­вимся на смысле этой диаграммы.

Рассмотрим, например, медь, которая создает в германии три акцепторных уровня, удаленных на 0,04 и 0,33 эВ от верха валентной зоны ,и на 0,26 эВ от дна зоны проводимости. Это зна­чит, что атом меди может присоединить к себе три электрона. При­соединение первого электрона (из числа электронов, обра­зующих валентные связи в кристалле) требует наименьшей энергии Е₁ — E_v = 0,04 эВ. При этом атом меди превращается в отрицательный ион Сu^- и одновремейно образуется подвижная положительная дырка. Поэтому мы можем также сказать, что этот электронный переход есть отрыв связанной дырки от акцептора, на что необходима энергия ионизации 0,04 эВ. Для отрыва захвачен­ного электрона от иона Сu^- и перевода его в подвижное состояние необходима наименьшая энергия 0,79—0,04 = 0,75 эВ, где 0,79 эВ есть ширина запрещенной зоны германия (при 0К). Аналогично, энергия Е₂ — E_v = 0,33 эВ на этой диаграмме есть приращение энергии центра при присоединении к иону Сu^- второго электрона (Из числа электронов связи) и превращении его в ион Сu^2-. При этом среди электронов связи (в валентной зоне) образуется вторая подвижная дырка, и мы можем сказать, что энергия 0,33 эВ есть энергия отрыва второй дырки, связанной с ионом Сu^-. Энергия отрыва электрона от иона Сu^2- есть 0,79 — 0,33 = 0,46 эВ. И, нако­нец, энергия присоединения третьего электрона, теперь уже к иону Сu^2- (или что тоже, энергия отрыва третьей дырки), равна Е₃ — E_v = 0,79 — 0,26 = 0,53 эВ. При этом образуется ион Сu^3-. Энергия отрыва захваченного третьего электрона есть E_с — Е₃ = = 0,26 эВ. Таким образом, узельные атомы меди в германии яв­ляются тройными акцепторами и могут существовать в четырех зарядных состояниях: Сu⁰, Сu^-, Сu^2- и Сu^3-.

Число различных локальных уровней энергии для узельных примесных атомов в германии в ряде случаев согласуется с ожи­даемым на основании электронной структуры атома и тетраэдрического характера валентных связей в германии. Рассмотрим, напри­мер, элементы II группы Zn и Cd. Их атомы имеют по два валентных электрона: (4s)² и, соответственно, (5s)². Однако для образования завершенных тетраэдрических связей в германии необходимо четыре электрона. Недостаток двух электронов приводит к образованию двух дырок, связанных с этими атомами, и поэтому они являются двойными акцепторами.

Рис. 2.20. Энергетические уровни некоторых примесей в германии при темпе­ратуре абсолютного нуля. Все уровни — акцепторные, за исключением наинизшего уровня золота.

Элементы Мn (VII группа) и Fe, Co, Ni (VIII группа) все имеют на самой внешней оболочке по два электрона (4s)². По-видимому, именно эта пара электронов и участвует в образовании валентных связей. Но тогда опять для завершения валентных связей не хва­тает двух электронов, и атомы этих элементов тоже являются двой­ными акцепторами.

Элементы I группы Сu, Ag и Аu имеют по одному валентному электрону: (4s), (5s) и (6s). Поэтому при узельном положении этих атомов с ними связаны три дырки, и они являются тройными акцеп­торами. Однако у Аu обнаруживается еще и донорный уровень, связанный с возможностью отщепления валентного электрона. Рассмотрим, наконец, еще пример Те (VI группа). Он имеет шесть валентных электронов (5s)² (5p)⁴, в то время как для завер­шения валентных связей их необходимо только четыре. В соответ­ствии с этим узельные атомы теллура создают в германии два донорных уровня.

32) Мелкие и глубокие уровни.

Примесными уровнями называются энергетические состояния полупроводника. расположенные в запрещенной зоне и обусловленные присутствием в нем примесей и структурных дефектов. В зависимости от того, мало или сравнимо с шириной запрещенной зоны расстояние от примесного уровня до ближайшей разрешенной зоны, различают мелкие и глубокие примесные уровни. По способности примесного атома отдавать электрон в зону проводимости либо принимать его из валентной зоны примесные уровни разделяют на донорные и акцепторные.

Мелкие примесные уровни, соответствующие примесям замещения (замещение атома кристалла примесным атомом), проявляют донорный характер, если валентность примесного атома превышает валентность атомов основного элемента, и акцепторной − при обратном соотношении. Глубокие примесные уровни обычно образуются при замещении атомов основного вещества атомами, отличающимися по валентности более чем на . Такие примеси иногда способны образовывать несколько примесных уровней, соответствующих различным зарядовым состояниям, например, атомы меди в германии создают три примесных уровня, соответствующих ионам Cu^1-, Cu^2- и Cu^3-. Глубокие примесные уровни, отвечающие разным ионам, могут иметь различный характер (одни могут быть донорными, другие − акцепторными).

Донорный уровень называется мелким, если его энергия (отсчитываемая от дна зоны проводимости) сравнима с характерной энергией теплового движения при комнатной температуре , где - температура, а - постоянная Больцмана. Эта энергия составляет примерно 26 мэВ. Мелкими донорами могут быть не только примесные атомы, но и комплексы структурных дефектов (например т.н. термодоноры в кремнии). Многие примеси и точечные дефекты, (например золото и медь в кремнии) вакансии, являются глубокими донорами.

33) Водородоподобные примес­ные центры.

Водородоподобными примесными центрами являются атомы, состоящие, подобно атому водорода, из ядра и одного электрона. Такими являются ионизованные атомы, потерявшие все электроны, кроме одного, например, Не⁺, В³⁺ и т. д. Водородоподобные атомы обладают сходными с водородом оптическими свойствами. В физике полупроводников их называют примесными атомами, у которых валентность на 1 больше или меньше, чем у основных атомов.

Например, в кристаллах элементов IV группы периодической системы элементов (кремнии, германии) однозарядными донорами являются элементы V группы: фосфор, мышьяк, сурьма. Так как элементы пятой группы обладают валентностью 5, то четыре электрона образуют химическую связь с четырьмя соседними атомами кремния в решётке, а пятый электрон оказывается слабо связанным (энергия связи порядка нескольких сотых электрон-вольта) и образует так называемый водородоподобный примесный центр, энергию которого просто оценить из решения уравнения Шрёдингера для атома водорода, принимая во внимание, что электрон в кристалле — квазичастица и его эффективная масса отличается от массы электрона, а также, что электрон движется не в вакууме, а в среде с некой (порядка 10) диэлектрической проницаемостью.

42) Проводимость, постоянная Холла и термо-ЭДС.