Трёхмерные дефекты

Объёмные дефекты. К ним относятся скопления вакансий, образующие поры и каналы; частицы, оседающие на различных дефектах (декорирующие), например пузырьки газов, пузырьки маточного раствора; скопления примесей в виде секторов (песочных часов) и зон роста. Как правило, это поры или включения примесных фаз. Представляют собой конгломерат из многих дефектов. Происхождение — нарушение режимов роста кристалла, распад пересыщенного твердого раствора, загрязнение образцов. В некоторых случаях (например, при дисперсионном твердении) объемные дефекты специально вводят в материал, для модификации его физических свойств.

Дефекты без сомнения оказывают сильное воздействие на свойства заголовки. Но далеко не всегда это нежелательные воздействия связанные с потерей материалом нужных характеристик. Часто кристаллическую решетку специально подвергают изменениям, чтобы добиться нужных свойств.

Точечные дефекты такие как атомы внедрения и атомы замещения используются для так называемого легирования, то есть подмешивание в состав материала примесей других элементов. Например, при легировании кремния фосфором можно получить полупроводник с n-типа , величина примеси будет также влиять на плавность p-n перехода. В противоположность этому легирование кремний бором даст полупроводник с n-типом проворности. Для получения качественной стали с высокими показателями долговечности железо легируют углеродом и марганцем.

Дислокация относящиеся к линейным дефектам позволяют увеличивать прочность материала однако при этом происходит потеря пластичности, но иногда именно это и требуется.

21) Основные приближения зонной теории.

Как известно из квантовой механики, для теоретического иссле­дования любой системы частиц, в частности для вычисления воз­можных значений ее энергии, надо решить соответствующее урав­нение Шредингера. Последнее представляет собой дифференциаль­ное уравнение в частных производных, содержащее столько пере­менных, сколько степеней свободы имеет рассматриваемая система. В физике твердого тела в эту систему входят, строго говоря, все электроны и атомные ядра атомов, составляющих кристалл. Таким образом, число степеней свободы, а с ним и число переменных в урав­нении Шредингера, оказывается макроскопически большим — по­рядка 10²² - 10²³. В результате взаимодействия между частицами переменные не разделяются, и мы приходим к математической за­даче исключительной трудности. Прямое решение ее в настоящее время невозможно. Более того, даже если бы решение поставленной задачи удалось найти, физическая интерпретация его представила бы, видимо, не меньше трудностей, чем сам процесс решения, ибо объем информации, таким путем полученной, был бы необычайно велик.

По этим причинам современная квантовая теория твердого тела вынуждена основываться на ряде упрощений. Последние выбираются с таким расчетом, чтобы сохранить лишь наиболее характерные черты системы, исключив все, сравнительно мало существенное. Зонная теория (смысл названия будет ясен из даль­нейшего) представляет собой, по-видимому, самую простую кван-товомеханическую схему, учитывающую наиболее важные особен­ности движения электронов во многих кристаллах. Как мы увидим, она позволяет успешно интерпретировать ряд экспери­ментальных данных.

Зонная теория базируется на следующих основных предполо­жениях, составляющих в своей совокупности так называемое «зон­ное приближение»:

1) При изучении движения электронов атомные ядра, ввиду их большой массы, рассматриваются как неподвижные источники поля, действующего на электроны.

2) Расположение ядер в пространстве считается точно перио­дическим: они размещаются в узлах идеальной решетки данного кристалла.

3) Взаимодействие электронов друг с другом заменяется неко­торым эффективным внешним полем. Иначе говоря, система элек­тронов, взаимодействующих с атомными ядрами и друг с другом по закону Кулона, заменяется системой независимых электронов, движущихся в некотором заданном поле. Последнее складывается из поля атомных ядер и эффективного поля, приближенно описы­вающего взаимодействие между электронами.

Первое предположение позволяет рассматривать поведение элек­тронов, не интересуясь движением тяжелых частиц. Эта возмож­ность не является самоочевидной, ибо в результате взаимодействия между электронами и ядрами движения их не независимы: строго говоря, расположение, ядер не задано, а изменяется с изменением состояния электронов. Смысл предположения 1) заключается в ут­верждении, что последний эффект мал.

Второе предположение ограничивает класс рассматриваемых систем: речь идет о кристаллических твердых телах, а не о жидко­стях, стеклах и т. п.

Наконец, третье предположение сводит многоэлектронную за­дачу к одноэлектронной. Вместо одного уравнения Шредингера для всей системы атомных ядер и электронов мы получаем теперь сово­купность идентичных, не связанных между собой уравнений Шре­дингера для каждого электрона в отдельности.

22) Волновая функция электрона в периодическом поле кристалла.

Обозначим потенциальную энергию элек­трона в нем через U (r), где r (х, у, z) — радиус-вектор данной точки пространства. Явный вид функции U (r) нам пока неизвестен. Однако многие важные особенности рассматриваемой системы можно выяснить, не задавая явного вида U (r), а пользуясь лишь некоторыми общими свойствами этой функции.

Для выяснения свойств функции U (r) заметим, прежде всего, что наша система зарядов в целом нейтральна: полный заряд валент­ных электронов равен по величине и противоположен по знаку заряду всех атомных остовов. Далее, следует ожидать, что не только остовы, но и электроны будут расположены в пространстве в среднем периодически. (В дальнейшем это будет показано явно.) Следовательно, и поле, создаваемое данной системой зарядов, должно быть периодично в пространстве:

U(r) = U(r + a_n), (2.1)

т. е. потенциальная энергия электрона в кристалле инвариантна относительно сдвига на вектор решетки а_n. Итак, мы пришли к задаче о движении электрона в периодическом поле.

В этой главе будут рассматриваться только стационарные состояния электронов. Соответственно уравнение Шредингера имеет вид

Нψ = Еψ. (2.2)

Здесь Н — оператор энергии (гамильтониан) рассматриваемой си­стемы, Е — его собственные значения, а ψ есть волновая функция — собственная функция оператора Н, принадлежащая собственному значению Е. В рассматриваемой нами задаче оператор Н представ­ляет собой сумму операторов потенциальной энергии электрона U и кинетической энергии р²/2m₀. Здесь т₀ есть масса свободного элек­трона, а р — оператор импульса:

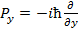, , (2.3)

т. е.

(2.3')

Через ћ, как обычно, обозначена постоянная Планка h, деленная на 2л.

В соответствии со сказанным уравнение (2.2) применительно к задаче об электроне в периодическом поле принимает вид

(2.4)

причем функция U (г) обладает свойством (2.1).

Коль скоро потенциальная энергия U (г) не зависит от спина электрона, каждым собственному значению энергии Е и координат­ной волновой функции ψ отвечают два состояния, соответствующие двум возможным ориентациям спина. Об этом говорят как о спино­вом вырождении.

При наложении магнитного поля B спиновое вырождение сни­мается, ибо энергия электрона становится зависящей от проекции магнитного момента на направление B. В отсутствие магнитного поля спиновое вырождение играет роль только при подсчете общего числа дозволенных квантовых состояний, приводя к появлению дополнительного множителя 2.

Определив из уравнения (2.4) волновую функцию ψ, мы можем найти средние значения любых физических величин, характери­зующих поведение электрона. В частности, выражение

|ψ (r)|²dr (2.7)

дает нам вероятность обнаружить электрон в элементе объема dr = dx dy dz около точки r. По смыслу понятия вероятности должно выполняться условие нормировки

=1. (2.8) где интеграл берется по всему объему системы.

Условие сходимости этого интеграла играет роль одного из до­полнительных условий к уравнению (2.4): физически допустимы только те решения, для которых интеграл (2.8) сходится.

Произведем в уравнении (2.4) замену аргумента

r = r' + а_n.

Принимая во внимание равенство (2.1) и опуская штрих у пере­менной г', получаем

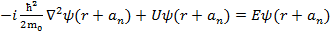(2.4')

Сравнивая это с (2.4), видим, что функции ψ (r) и ψ (r + а_n) удов­летворяют одному и тому же уравнению Шредингера с одним и тем же собственным значением энергии Е. Если этому собственному значению принадлежит одна собственная функция (т. е. если это собственное значение не вырождено), то функции ψ (r) и ψ (r + а_n) могут отличаться лишь постоянным множителем:

ψ(r + а_n) = c_n ψ(r). (2-9)

Поскольку обе они должны быть нормированы, абсолютная вели­чина с_n должна быть равна единице:

|с_n| = 1. (2.10)

Таким образом,

| ψ (r + а_n)|² = | ψ (r)|² (2.11)

— электрон с одинаковой вероятностью может быть обнаружен в элементе объема dr как около точки r, так и около любой эквива­лентной ей точки r + а_n. Иначе говоря, как мы и ожидали, среднее (в квантовомеханическом смысле) распределение электронов в решетке обладает пространственной периодичностью последней.

Легко найти явный вид зависимости с_n от вектора а_n. Для этой цели произведем в уравнении (2.4) два последовательных сдвига аргумента — на а_n и а_n', где вектор а_n' отличается от а_n заменой чисел п₁, п₂, п₃ на п₁’, n'₂, n'₃. Применяя дважды соотношение (2.9), получим

ψ (r + а_n + а_n')= с_n с_n ψ (r). (2.12')

С другой стороны, по определению

а_n + а_n' =а_n+n' и, следовательно,

ψ (r + а_n + а_n')= ψ (r + а_n+n' ) = с_n+n’ ψ (r) (2.12")

Сравнивая равенства (2.12') и (2.12"), находим

С_пС_n'=С_{п + п'}. (2.13)

Прямой подстановкой легко убедиться, что это функциональное уравнение имеет решение

С_n = е ^ika_n (2.14)

где к — произвольный вектор. В силу равенства (2.10) компоненты к должны быть вещественными.

Равенство (2.14) с сочетании с (2.11) позволяет в известной мере раскрыть вид функций ψ (r), удовлетворяющих уравнению Шредингера периодическим потенциалом U (г). Именно, легко убе­диться, что

ψ (r) = e ^ikr u_k(r),(2.15)

где u_k (r) — функция, периодическая с периодом решетки:

u_k(r) = u_k(r + а_n). (2-16)

Действительно, в силу (2.11) ψ (r) может отличаться от функции, периодической с периодом решетки, только фазовым множителем вида e^if(r), где f — вещественная функция. В силу (2.14) она должна быть линейной.

Равенства (2.15), (2.16) составляют содержание теоремы Блоха: волновая функция электрона, движущегося в периодическом поле, представляет собой модулированную плоскую волну. Иначе говоря, это есть произведение экспоненциальной функции e^ikr на функцию, периодическую с периодом решетки. Сами функции вида (2.15), (2.16) иногда называют функциями Блоха.

Вектор к называют квазиволновым. Очевидно, его компоненты имеют размерность [см^-1]. Обычно к пишут в виде

, (2.17)

где р — вектор размерности импульса. Он называется квазиимпульсом.

Вектор р в данном случае есть обычный импульс, связанный с энергией Е равенством

(2.20)

Из формулы (2.17) непосредственно вытекает соотношение де Бройля, связывающее импульс с волновым вектором:

P = ћk

23) Зона Бриллюэна.

Вектор р (или к = р/ћ) характеризует закон преобразования волновой функции электрона при сдвиге ее аргумента на какой-либо вектор решетки. Разным собственным функ­циям соответствуют, вообще говоря, различные значения квази­импульса (квазиволнового вектора). Поэтому компоненты его (как и компоненты импульса в случае свободного электрона) следует рассматривать как квантовые числа, характеризующие данное ста­ционарное состояние. Однако, в отличие от компонент импульса и от квантовых чисел, встречающихся в теории атома, квазиимпульс определяется в принципе неоднозначно. Действительно, обозначим через с вектор, скалярное произведение которого на а_n есть целое кратное 2лй:

а_nс = 2лН x (целое число). (3.2)

Следовательно, век­торы р и р + с физически эквивалентны: оба они определяют одно и то же преобразование волновой функции.

Нетрудно найти явный вид вектора с. Для этого следует лишь ввести понятие обратной решетки. Основные векторы последней b₁, b₂, b₃ определяются равенствами

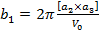, , (3.3)

где V₀ = | (а₁ [а₂ 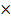а₃]) | есть объем параллелепипеда, построенного на векторах a₁, a₂, а₃ (объем элементарной ячейки). В частности, в простой кубической решетке, когда а₁ = а₂ = а₃ = а и b₁ = b₂ = b₃ = b, мы имеем

(3.3')

Очевидно, векторы b₁, b₂, b₃ имеют размерность обратной длины. На основных векторах b₁,b₂, b₃ можно построить периодическую решетку. Она и называется обратной (по отношению к прямой ре­шетке данного кристалла).

Произвольный вектор обратной решетки имеет вид

b_m = m₁b₁ + m₂b₂ + m₃b₃, (3.4)

где т₁, т₂, т₃ — положительные или отрицательные целые числа или нули (при этом т₁, т₂ и т₃ не равны нулю одновременно), т = { т₁, т₂, т₃ }.

Элементарная ячейка обратной решетки представляет собой параллелепипед, построенный на векторах b₁, b₂, b₃. «Объем» этого параллелепипеда равен | (b₁ [b₂ x b₃]) | (разумеется, он имеет размерность обратного объема). Подставляя сюда формулы (3.3) для b₁, b₂, b₃ и раскрывая получающееся произведение, находим

|(b₁ [b₂ х b₃]) | = (2π)³/V₀. (3.5)

Как и в случае прямой решетки, выбор элементарной ячейки в обратной решетке неоднозначен и определяется соображениями удобства.

Другой способ построения элементарной ячейки состоит в сле­дующем. Какой-то узел обратной решетки выбирают в качестве начала координат и соединяют его прямыми линиями с ближайшими к нему узлами. Через середины этих линий перпендикулярно к ним проводят плоскости. В качестве элементарной ячейки обратной решетки можно выбрать наименьший многогранник, ограниченный так построенными плоскостями и содержащий внутри себя начало координат. Этот многогранник называется ячейкой Вигнера — Зейтца.

Такие многогранники можно построить около любого узла ре­шетки; при этом они не перекрываются и совокупность их заполняет все обратное пространство. Отсюда следует, что объем одного много­гранника действительно равен (2π)³/V₀, как это и должно быть. В отличие от параллелепипеда, построенного на векторах b₁, b₂, b₃, элементарная ячейка, выбранная указанным только что образом, обладает всеми свойствами симметрии обратной решетки.

Из определения (3.3) вытекают равенства

а₁b₁ = а₂b₂ = а₃b₃ = 2π,

а_αb_β = 0, α ≠ β (α, β = 1,2,3).

Умножим теперь произвольный вектор решетки на век­тор обратной решетки (3.4). Пользуясь соотношениями (3.6), мы получаем

a_nb_m = (п₁т₁ + п₂т₂ + п₃т₃) 2π.

В скобках в правой части этого равенства стоит целое число, и, сле­довательно, вектор с, удовлетворяющий условию (3.2), можно записать в виде

с = ћ b_m. (3.7)

Итак, квазиимпульс определен лишь с точностью до вектора обратной решетки, умноженного на ћ. Это обстоятельство позволяет ограничить изменение компонент квазиимпульса конечной областью, исчерпывающей все физически неэквивалентные их значения. Такая область — совокупность всех физически неэквивалентных значений квазиимпульса — называется зоной Бриллюэна. В силу произвольности вектора b_т в (3.7) выбор ее неоднозначен. Так, можно выбрать в качестве зоны Бриллюэна область, определяемую неравенствами

— π ћ < ра₁ ≤ π ћ,

— π ћ < ра₂ ≤ π ћ, (3.8)

— π ћ <ра₃ ≤ π ћ.

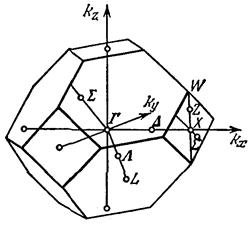Рис. 3.1. Первая зона Бриллюэна для решеток типа алмаза и цинко­вой обманки.

Эти неравенства определяют некоторый параллелепипед в p-пространстве, содержащий в себе начало координат. Его называют первой зоной Бриллюэна. Можно определить первую зону Бриллюэна и для компонент квазиволнового вектора k: надо лишь заменить р на k в неравен­ствах (3.8), опустив множители ћ. Квазиимпульс (или квазиволновой вектор), изменяющийся впределах первой зоны Бриллюэна, называется приведенным. В частности, в простой кубической ре­шетке векторы а1,а2, а3 одинаковы по величине (равной постоянной решетки а) и направлены по трем взаимно перпендикулярным осям куба. Выбирая эти оси в качестве координатных, получаем из (3.8) для данного частного случая а = х, у, z. (3.8’)

Первая зона Бриллюэна здесь представляет собой куб объема . В k-пространстве соответствующий объем равен (2π)³/V₀.

Выбирая другие периоды р_x, р_y, p_z, мы получим вторую, третью и т. д. зоны Бриллюэна.

Таким образом, зона Бриллюэна есть чисто геометрическое по­нятие: форма ее зависит только от структуры решетки, но не от природы действующих в ней сил. Более того, как видно из предыду­щего, зона Бриллюэна определяет­ся только основными векторами решетки. Следовательно, она одна и та же как для простых, так и для базисных решеток одной и той же сингонии, например для простой гранецентрированной ре­шетки и для решетки типа алмаза.

24) Энергетические зоны.

25) Эффективная масса.

В физике твёрдого тела, эффективной массой частицы называется динамическая масса, которая появляется при движении частицы в периодическом потенциале кристалла. Можно показать, что электроны и дырки в кристалле реагируют на электрическое поле так, как если бы они свободно двигались в вакууме, но с некой эффективной массой, которую обычно определяют в единицах массы покоя электрона m_e (9.11×10⁻³¹ кг). Она отлична от массы покоя электрона.

Эффективная масса определяется из аналогии со вторым законом Ньютона . С помощью квантовой механики можно показать, что для электрона во внешнем электрическом поле E:

где — ускорение, — постоянная Планка, — волновой вектор, который определяется из импульса как = , — закон дисперсии, который связывает энергию с волновым вектором . В присутствии электрического поля на электрон действует сила , где заряд обозначен q. Отсюда можно получить выражение для эффективной массы :

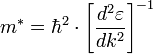
Для свободной частицы закон дисперсии квадратичен, и таким образом эффективная масса является постоянной и равной массе покоя. В кристалле ситуация более сложна и закон дисперсии отличается от квадратичного. В этом случае только в экстремумах кривой закона дисперсии, там где можно аппроксимировать параболой можно использовать понятие массы.

Эффективная масса зависит от направления в кристалле и является в общем случае тензором.

Те́нзор эффекти́вной ма́ссы — термин физики твёрдого тела, характеризующий сложную природу эффективной массы квазичастицы (электрона, дырки) в твёрдом теле. Тензорная природа эффективной массы иллюстрирует тот факт, что в кристаллической решётке электрон движется не как частица с массой покоя, а как квазичастица, у которой масса зависит от направления движения относительно кристаллографических осей кристалла. Эффективная масса вводится, когда имеется параболический закон дисперсии, иначе масса начинает зависеть от энергии. В связи с этим возможна отрицательная эффективная масса.

По определению эффективную массу находят из закона дисперсии^[1]

где — волновой вектор, — символ Кронекера, — постоянная Планка.