Примесная проводимость

Для создания полупроводниковых приборов часто используют кристаллы с примесной проводимостью. Такие кристаллы изготавливаются с помощью внесения примесей с атомами трехвалентного или пятивалентного химического элемента.

По виду проводимости.Полупроводник n-типа

Этот вид полупроводников имеет примесную природу. В четырёхвалентный полупроводник (например, кремний) добавляют примесь пятивалентного полупроводника (например, мышьяка). В процессе взаимодействия каждый атом примеси вступает в ковалентную связь с атомами кремния. Однако для пятого электрона атома мышьяка нет места в насыщенных валентных связях, и он переходит на дальнюю электронную оболочку. Там для отрыва электрона от атома нужно меньшее количество энергии. Электрон отрывается и превращается в свободный. В данном случае перенос заряда осуществляется электроном, а не дыркой, то есть данный вид полупроводников проводит электрический ток подобно металлам. Примеси, которые добавляют в полупроводники, вследствие чего они превращаются в полупроводники n-типа, называются донорными.

Проводимость N-полупроводников приблизительно равна:

Полупроводник p-типа

Этот вид полупроводников, кроме примесной основы, характеризуется дырочной природой проводимости. В четырёхвалентный полупроводник (например, в кремний) добавляют небольшое количество атомов трехвалентного элемента (например, индия). Каждый атом примеси устанавливает ковалентную связь с тремя соседними атомами кремния. Для установки связи с четвёртым атомом кремния у атома индия нет валентного электрона, поэтому он захватывает валентный электрон из ковалентной связи между соседними атомами кремния и становится отрицательно заряженным ионом, вследствие чего образуется дырка. Примеси, которые добавляют в этом случае, называются акцепторными.

Проводимость p-полупроводников приблизительно равна:

Эффект Холла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле.В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле течёт электрический ток под действием напряжённости 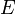. Магнитное поле будет отклонять носители заряда (для определённости электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости^[1] будет служить условие, что при этом электрон не начнёт двигаться по циклоиде.

Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска и положительного возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов не скомпенсирует магнитную составляющую силы Лоренца:

Скорость электронов можно выразить через плотность тока:

где — концентрация носителей заряда. Тогда

Коэффициент пропорциональности между и называется коэффициентом (или константой) Холла.

Термоэдс, электродвижущая сила, возникающая в электрической цепи, состоящей из нескольких разнородных проводников, имеющих в местах контактов различную температуру. Термо-ЭДС в полупроводниках, как и в металлах возникает под действием разности температуры. Основой преобразователей тепловой энергии в электрическую являются термоэлементы, составленные из последовательно включенных полупроводников p и n-типов. Большая термо-ЭДС полупроводников позволяет использовать их в качестве эффективных преобразователей тепловой энергии в электрическую.

43) Дрейфовая скорость, дрейфовая и холловская подвижности, фактор Холла.

Дрейфовая скорость — средняя скорость упорядоченного движения V, вызванная воздействием на электроны с помощью внешнего поля. В отсутствие внешнего электрического поля электроны в кристалле совершают только тепловое движение. Поэтому нет преимущественных направлений движения, и поэтому среднее значение тепловой скорости равно нулю.

Средняя скорость движения носителей зарядов в поле единичной напряженности называется подвижностью.

Подвижность носителей зарядов зависит от механизма их рассеяния в кристаллической решетке. Подвижности электронов (μn) и дырок (μp) в полупроводнике имеют различное значение (μn>μp) и определяются температурой и концентрацией примесей. Увеличение температуры приводит к уменьшению подвижности, что зависит от числа столкновений носителей зарядов в единицу времени.

Если к образцу полупроводника приложено внешнее электрическое поле вдоль оси ох, а также магнитное поле Н вдоль оси oz, то протекание тока вдоль оси ох приводит к появлению силы Лоренца и поля Холла, действующих вдоль оси оу. В отсутствие рассеяния возникает направленный (см. Холла эффект) дрейф вдоль оу, причём скорость дрейфа u_др пропорциональна полю Н. Коэффициент пропорциональности называется Xолловской подвижностью m_H.

Выражение для классической постоянной Холла получено в предположении, что все носители тока имеют одинаковую дрейфовую скорость движения , которая не изменяется при движении носителей заряда в веществе. В действительности, необходимо учитывать механизм рассеяния носителей заряда в твердом теле, что неизбежно приведет к уточнению значения постоянной Холла. В общем случае 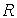определяется следующим выражением:

, где –Холл-фактор.

С помощью Холл-фактора учитываются разные механизмы рассеяния носителей заряда. При рассеянии на тепловых колебаниях решетки расчет дает значение . Это случай собственных полупроводников и полупроводников, имеющих носители заряда одного знака. В случае вырожденных полупроводников и металлов , а при преимущественном рассеянии на ионах примеси , Таким образом, в чистых полупроводниках с собственной проводимостью преобладает рассеяние на колебаниях решетки (например, в германии и кремнии при высоких и комнатных температурах), а для постоянной Холла получается выражение:

44) Дрейфовый и диффузионный ток.

Дрейфовый ток.Под действием электрического поля Е в кристалле полупроводника появляется упорядоченное движение — «дрейф» электронов и дырок, т.е. возникает электрический ток, называемый дрейфовым током. Согласно сказанному этот ток будет иметь электронную I_nдp и дырочную I_pдр составляющие:

I_др = I_nдр + I_рдр = s (j_nдр + j_рдр),

где s — поперечное сечение кристалла, см²; j_nдр, j_pдр — плотность электронного и дырочного дрейфового тока, А/см².

Плотность тока определяется электрическим зарядом q, проходящим через единичное поперечное сечение в единицу времени. Так как в одном кубическом сантиметре полупроводника содержится п электронов проводимости, что соответствует их концентрации, то при средней скорости дрейфа каждого электрона v_n в направлении, нормальном к рассматриваемому сечению, плотность электронного тока будет равна j_nдр = q_nvn = e_nvn. Рассуждая аналогично, получаем выражение для плоскости дырочного тока j_pдр = q_pvp = e_pvp.

Механизм дрейфа электронов проводимости в полупроводнике отличается от движения электронов в вакууме под действием силы электрического поля. В полупроводнике электроны проводимости, совершая тепловое хаотическое движение, испытывают столкновения с колеблющимися атомами кристаллической решетки, с атомами примесей и другими неоднородностями решетки. Столкновения не всегда носят упругий характер, например ионизированные атомы примеси могут захватывать электрон и высвобождать его через некоторый малый промежуток времени. Электрон, независимо от направления движения на длине свободного пробега l между двумя столкновениями, в результате воздействия электрического поля Е будет получать частичное смещение Δх в направлении действия сил этого поля. Следовательно, на хаотическое движение электрона проводимости за время Δt будет накладываться некоторое упорядоченное смещение Δх_ср в направлении, противоположном Е. Отношение Δx_cp/Δt = v_n представляет собой усредненную скорость электронов проводимости или скорость дрейфа. Если скорость дрейфа существенно меньше скорости теплового движения электронов, то она оказывается прямо пропорциональной напряженности электрического поля, т. е. v_n = μ_nE.

Коэффициент пропорциональности между этими величинами n, см²/(В*с) называется подвижностью электронов. Этот коэффициент численно равен средней скорости, приобретаемой электронами проводимости в кристалле, при напряженности электрического поля 1 В/см. При комнатной температуре для собственного полупроводника германия μ_n = 3900, для кремния μ_n = 1350 см/(В*с).Аналогичные процессы происходят и при дрейфе дырок в полупроводнике при воздействии на них электрического поля. Но так как механизм перемещения дырок связан фактически с перемещением валентных электронов, а не электронов проводимости, поэтому подвижность дырок оказывается меньше (примерно в 2 раза) подвижности электронов и составляет для германия μ_n = 1900, а для кремния μ_n = 500 см²/(В*с). Дырки и электроны проводимости, несущие разные по знаку заряды, дрейфуют в противоположных направлениях, создавая дрейфовые токи дырок и электронов одинакового направления.

Диффузионный ток. В полупроводниках электрический ток вызывается не только электрическим полем, но и Неравномерным распределением подвижных носителей заряда (электронов и дырок) по объему кристалла.

Пусть в некотором объеме полупроводника концентрация электронов проводимости слева от сечения аb больше, чем справа. Такую неравномерность концентрации подвижных носителей электрических зарядов в полупроводнике можно создавать и поддерживать неизменной при общей электрической нейтральности полупроводника в целом. Частицы совершают тепловые хаотические движения во всех направлениях, но, естественно, число частиц, движущихся из области с большой концентрацией в область с меньшей концентрацией, будет превышать число частиц, движущихся в противоположном направлении. В результате появится некоторое упорядоченное диффузионное перемещение электронов проводимости в направлении уменьшения их концентрации, т.е. возникнет диффузионный электрический ток, направление которого противоположно направлению диффузии электронов.

Плотность диффузионного тока j_пдиф прямо пропорциональна неравномерности концентрации электронов проводимости, называемой градиентом grad n_х ≈ Δn/Δx.

Аналогичный процесс происходит и при неравномерной концентрации дырок, создающей диффузионный электрический ток, совпадающий по направлению с направлением диффузии дырок (рис, 1-12, б). Из рис. 1-12, а, б следует, что диффузионный ток электронов совпадает по направлению с градиентом их концентрации, а диффузионный ток дырок направлен противоположно градиенту концентрации дырок. Плотность диффузионных токов в направлении оси х определяется соотношениями

j_пдифх = eD_n (Δn/Δx); j_рдифх = — eD_p (Δр/Δх),(1 -23)

где D_n и D_p —коэффициенты диффузии соответственно электронов и дырок.

Коэффициент диффузии подвижных носителей заряда в соответствии с формулами (1-23) равен количеству элементарных зарядов, диффундирующих через поперечное сечение 1 см² за одну секунду при единичном градиенте концентрации подвижных носителей зарядов. Знак минус в выражении (1-23) для дырочного тока указывает на его противоположное направление относительно grad p_x = Δр/Δх.

Коэффициенты диффузии связаны с подвижностями носителей соотношениями Эйнштейна

D_n = μ_nkT/e; D_p = μ_pkT/e.

При комнатной температуре kT/е ≈ 0,025. Учитывая численные значения μ_n и μ_р соответственно получаем: для германия D_n = 100, D_p = 49 см²/с; для кремния D_n = 30, D_p = 13cм²/c.

45) Соотношение Эйнштейна.

В физике (главным образом в молекулярно кинетической теории) соотношением Эйнштейна (также называемое соотношением Эйнштейна — Смолуховского) называется выражение, связывающее подвижность молекулы (молекулярный параметр) с коэффициентом диффузии и температурой (макро параметры). Оно было независимо открыто Альбертом Эйнштейном в 1905 году и Марианом Смолуховским (1906) в ходе работ по изучению броуновского движения:

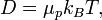
где 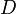— коэффициент диффузии, — подвижность частиц, — постоянная Больцмана, а

— абсолютная температура.

Величина подвижности определяется из соотношения

где — стационарная скорость перемещения частицы в вязкой среде под действием силы .

46) Механизмы рассеяния носителей заряда в неидеальной решетке.

РАССЕЯНИЕ НОСИТЕЛЕЙ ЗАРЯДА в кристаллич. твёрдых телах - процесс взаимодействия электрона проводимости (дырки) с нарушениями идеальной периодичности кристалла, сопровождающийся переходом электрона из состояния с импульсом p в состояние с импульсом . Рассеяние наз. упругим, если энергии электрона в начальном и конечном состояниях равны, или неупругим, если . Источником упругого рассеяния являются статич. дефекты - примесные атомы, дислокации, границы кристаллич. зёрен и т. п. (см. Дефекты в кристаллах). Осн. источником неупругого рассеяния являются колебания кристаллической решётки. Рассеяние электрона на колебаниях решётки описывается в терминах испускания и поглощения фононов движущимся электроном. Особое положение занимает Р. н. з. друг на друге.

При большой плотности носителей рассеяние ослабляется экранированием возмущения из-за перераспределения носителей в пространстве.

Возможно несколько механизмов рассеяния:

на фононах;

на примесях.

47) Взаимодействие носителей заряда с акустическими и оптическими фононами.

Рассеяние на фононах. Вероятность рассеяния электрона при испускании или поглощении фонона о импульсом q и энергией (без учёта принципа Паули) определяется выражением

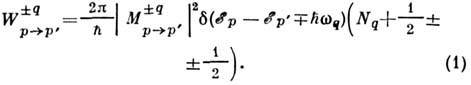
Здесь верх. и ниж. знаки соответствуют испусканию и поглощению фонона; числа фононов с импульсом q определяются распределением Планка (см. Планка закон излучения:)

Матричный элемент М перехода p → p' содержит закон сохранения квазиимпульса: (b - произвольный вектор обратной решётки). Переходы, для к-рых b = 0, наз. нормальными; если b.0, говорят о переходах с перебросом (см. Переброса процессы). Дельта-функция d отражает закон сохранения энергии. Вероятность рассеяния с испусканием фонона пропорц. N_q + 1. Два слагаемых, соответствующие N_q и 1, дают вероятности индуцированного и спонтанного рассеяний. Вероятность рассеяния с поглощением фонона пропорц. N_q, поэтому поглощение фонона всегда является индуцированным.

Рассеяние электрона на фононах в большой степени определяется законами сохранения энергии и импульса (кинематич. факторы), а также принципом Паули. Поэтому картина рассеяния различна для акустич. и оптич. фононов, имеющих разные законы дисперсии , и зависит от степени вырождения электронного газа. Кинематика позволяет установить, какие фононы дают осн. вклад в рассеяние, какова степень упругости рассеяния, а также является ли оно индуцированным или спонтанным.

Рассеяние на акустических фононах в полупроводниках. Т. к. скорость электрона v имеет порядок скорости звука s только при очень малой его энергии ( ! ms² ! 0,1 К), то в реальных условиях Это означает, что возмущение, создаваемое акустич. фононом, почти статично, а рассеяние электронов всегда квазиупруго. Из кинематики следует, что осн. вклад в рассеяние вносят фононы с импульсом ; поэтому

направленный импульс электрона теряется всего за неск. столкновений. Энергия фонона с таким импульсом ! 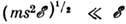, так что для релаксации энергии требуется много столкновений, т. е. действительно

Является ли рассеяние индуцированным или спонтанным, зависит от соотношения между энергией фонона hsp и тепловой энергией Т. Эти величины сравниваются, когда энергия электрона равна Если то характерны N_q 1; доминирует спонтанное испускание фононов (динамич. трение), и "движение" электрона по оси энергии 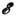есть систематич. дрейф вниз. При доминируют индуциров. переходы, т. к. При этом испускание происходит не намного чаще, чем поглощение, и "движение" электрона по оси энергий превращается в диффузию.

Рассеяние на акустических фононах в металлах и вырожденных полупроводниках. Вследствие закона сохранения импульса наиб. вероятно взаимодействие с фононами, импульс к-рых , где - импульс Ферми (см. Ферми-поверхность ).Но испусканию таких фононов (с энергией ) может препятствовать принцип Паули, если превышение энергии электрона над энергией Ферми много меньше 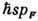, а поглощение может ослабляться из-за малого числа таких фононов, если . Поэтому характер рассеяния сильно зависит от Г и превышения энергии электрона над энергией Ферми. При почти для всех электронов (указанные ограничения несущественны) и рассеяние (с испусканием и поглощением) идёт на фононах с и энергией . Для релаксации импульса требуется неск. столкновений, а для релаксации энергии - много (квазиупругое рассеяние). При поглощение фононов с энергией маловероятно, но если , то принцип Паули не запрещает испускание таких фононов (в осн. спонтанное). Рассеяние, как и при высоких темп-pax, квазиупруго. Если же , то принцип Паули разрешает только испускание фононов с . Такое рассеяние является малоугловым, и выравнивание распределения электронов на поверхности Ферми происходит диффузионно. Для полной релаксации импульса требуется много столкновений, релаксация же энергии происходит за неск. столкновений (неупругое рассеяние).

Рассеяние на оптических фононах. При рассеянии в металлах существенны оптич. фононы во всей зоне Бриллюэна, в осн. коротковолновые с , где b₀ - размер Бриллюэна зоны. В полупроводниках в рассеянии участвуют только оптич. ДВ-фононы с . Частоту этих фононов w₀ можно считать не зависящей от q. Рассеяние на оптич. фононах квазиупруго только при ! 400 К, т. е. только при очень высоких энергиях электронов (см. Горячие электроны ).В области энергий проявляются неупругий и пороговый характеры рассеяния. Это существенно при низких темп-pax , когда ниже порога ( ) рассеяние слабое и возможно только за счёт маловероятного поглощения фонона, пропорционального , а выше порога ( ) рассеяние сильное - оно происходит при спонтанном испускании фонона.

48) Рассеяние носителей заряда на заряженных и нейтральных примесях.

При рассеянии на примесных атомах возмущение dV обусловлено элект-рич. полем (если примесь заряжена) и деформацией решётки в окрестности примеси. Иногда нужно учитывать обменные силы и магн. момент примеси. В случае заряж. примесей (примесных ионов) в полупроводниках вклад в dV от деформации решётки несуществен. Т. к. в полупроводнике p b₀, где b₀ - размер зоны Бриллюэна, то изменение импульса электрона при упругом рассеянии мало, а это значит, что рассеяние на больших расстояниях (r а₀) определяется сглаженным потенциалом dV(r). Такой потенциал не зависит от микроструктуры примеси и имеет кулоновский вид:

где Ze - заряд иона. Поэтому время релаксации импульса можно вычислить, пользуясь Резерфорда формулой для сечения рассеяния заряж. частиц. Согласно этой ф-ле, дифференц. сечение рассеяния электрона под углом в телесном угле dW:

где u - скорость электрона. Для вычисления необходимо усреднить s по всем 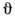. При интегрировании (12) по получают расходящийся интеграл, т. е. бесконечно большое сечение рассеяния. В действительности сечение рассеяния на примесном ноне конечно, т. к. кулоновский характер поля dV на больших расстояниях от примеси искажается полем др. примесных ионов и экранирующим полем электронов. Если учитывать первый фактор и "обрезать" кулоновский потенциал на ¹/₂ расстояния между примесными центрами, равного N^-1/3(N - концентрация примесей), то это приводит к ф-ле

Здесь - боровская энергия, F = In

Ф-ла (13) носит назв. Конуэлл - Вайскопфа формулы.

Если учитывать также экранирование кулоновского поля примесного иона свободными носителями заряда, то обрезание потенциала осуществляется его умножением на ехр(-r/l), где l - длина экранирования. При этом в ф-ле (13) F = ln(1- х) - х²/(1 + x²), где x = 2p/l (Брукса - Херринга формула).

Рассеяние на нейтральных примесях в полупроводниках обусловлено кулоновскими и обменными силами, действующими между рассеивающимся электроном и атомом примеси. Используя аналогию с рассеянием на атоме водорода, обычно пользуются т. н. ф-лой Эргинсоя:

где - боровский радиус, С = 20.

49) Генерация и рекомбинация неравновесных носителей заряда.

Образование свободных носителей заряда в полупроводниках связано с переходом электронов из валентной зоны в зону проводимости. Для осуществления такого перехода электрон должен получить энергию, достаточную для преодоления запрещенной зоны.

Однако помимо теплового возбуждения появление свободных носителей заряда может быть связано с другими причинами, например, в результате облучения фотонами или частицами большой энергии, ударной ионизации, введения носителей заряда в полупроводник из другого тела (инжекция) и др. Возникшие таким образом избыточные носители заряда называются неравновесными. Таким образом, полная концентрация носителей заряда равна:

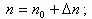(1.31)

(1.32)

где n₀ и p₀ - равновесная концентрация, а Δn и Δp - неравновесная концентрация электронов и дырок. Если возбуждение избыточных электронов производилось из валентной зоны, а полупроводник однородный и не содержит объемного заряда, то концентрация избыточных электронов равна концентрации избыточных дырок:

(1.33)

После прекращения действия механизма, вызвавшего появление неравновесной концентрации носителей, происходит постепенное возвращение к равновесному состоянию. Процесс установления равновесия заключается в том, что каждый избыточный электрон при встрече с вакантным местом (дыркой) занимает его, в результате чего пара неравновесных носителей исчезает. Явление исчезновения пары носителей получило название рекомбинации. В свою очередь возбуждение электрона из валентной зоны или примесного уровня, сопровождающееся появлением дырки, называется генерацией носителей заряда.

На рисунке 1.9 G - это темп генерации, а R - темп рекомбинации свободных носителей заряда в собственном полупроводнике.

Рис. 1.9. Генерация и рекомбинация свободных электронов и дырок в полупроводниках

Скорость (темп) рекомбинации R пропорциональна концентрации свободных носителей заряда:

(1.34)

где γ - коэффициент рекомбинации. При отсутствии освещения (в темноте) G=G₀ и , величины n₀ и p₀ иногда называют темновыми концентрациями свободных электронов и дырок соответственно. Из формул (1.30) и (1.14) получим:

(1.35)

где E_g = E_C - E_V - ширина запрещенной зоны. Таким образом, G₀ будет больше в узкозонных полупроводниках и при высоких температурах.

Если в полупроводнике нет электрического тока и объемных зарядов, то изменение во времени неравновесных концентраций электронов и дырок в зонах определяется уравнениями:

(1.36)

Скорости (темпы) генерации и рекомбинации имеют две составляющие:

(1.37)

где ΔG, ΔR - темпы генерации и рекомбинации только неравновесных электронов, то есть ΔG - это темп генерации электронов и дырок за счет освещения полупроводника, R₀ = γn₀p₀ и ΔR = γ·Δn·Δp. Используя равенство (1.31), (1.32) и (1.34), уравнение (1.36) можно свести к следующему:

(1.38)

Рассмотрим процесс рекомбинации неравновесных носителей заряда (то есть при выключении освещения в момент времени t = 0). Общее решение уравнения (1.38) довольно сложное. Поэтому рассмотрим два частных случая.

В собственном полупроводнике при сильном освещении Δn >> n₀+p₀. Из (1.38) получим:

(1.39)

где Δn₀ - начальная концентрация неравновесных носителей заряда. Спад концентрации происходит по параболическому закону.

В донорном полупроводнике в случае полной ионизации доноров n₀ = N_D, p₀ << n₀. Будем также считать, что Δn << N_D. Уравнение (1.38) сводится к виду: (1.40)

где введено обозначение: (1.41)

Уравнение (1.40) легко решается: (1.42)

Величина τ имеет смысл среднего времени электронов в зоне проводимости. Полученные решения иллюстрируются на рисунке 1.10. Из (1.42) видно, что процесс рекомбинации описывается экспоненциальной зависимостью от времени, причем среднее время жизни представляет собой такой отрезок времени, за который концентрация избыточных носителей изменяется в "е" раз.

50)Уравнение кинетики реком­бинации.

Взаимодействие электрона и дырки может приводить к их рекомбинации, в результате которой электрон возвращается в валентную зону, а энергия, затраченная на переброс электрона из валентной зоны в зону проводимости, выделяется в виде излучения или тепла. Если полупроводник находится в равновесных условиях, то число носителей заряда, возникающих в нем в результате тепловой генерации, равно числу носителей, исчезающих в результате рекомбинации и равновесная концентрация носителей не изменяется. Соответствующее кинетическое уравнение, характеризующее изменение концентрации носителей заряда, можно записать в следующем виде:

где G и U - соответственно, скорость генерации и скорость рекомбинации, n - концентрация электронов в данный момент времени, n₀ - равновесная концентрация электронов, G - генерационный член (число электронов, генерируемых в единице объема в единицу времени), τ_n - характеристическое время жизни, Δn - избыточная над равновесной концентрация носителей заряда. Решение этого уравнения имеет вид: (22)

где A зависит от начальных условий. Аналогичные соотношения можно записать для дырок:

(23)

51) Времена жизни.

В соответствии с (22, 23) константы τ_n и τ_p (время жизни электронов и дырок) можно определить как время, в течение которого концентрация неравновесных (избыточных) носителей заряда убывает в e раз. Поскольку мы говорим избыточных, следовательно, время измеряется после снятия возбуждения. Таким образом, время жизни характеризует длительность пребывания в разрешенной зоне неравновесных носителей заряда.

Вероятность того, что электрон столкнется с дыркой за единицу времени равна:

(1)

Так как столкновение с дыркой заканчивается рекомбинацией, то представляет собой вероятность рекомбинации электрона за единицу времени, а величина обратная , выражает среднее время жизни электрона в свободном состоянии:

Величина - называется коэффициентом рекомбинации электронов.

Существует несколько механизмов рекомбинации, часто говорят, каналов. Все эти каналы работают параллельно, поэтому существует некоторое эффективное время жизни, для которого, учитывая, что все каналы рекомбинации независимые, можно написать:

(24) где τ_ef - эффективное время жизни электронов (или дырок), τ_i - время жизни, характеризующее i-й канал. Как видно из (22), если скорости рекомбинации по различным каналам значительно отличаются, то эффективное время жизни будет определяться тем каналом, для которого время жизни минимально.

52) Фотопроводимость.

- фоторезистивный эффект, увеличение электропроводности полупроводника под действием электромагн. излучения. Впервые Ф. наблюдалась в Se У. Смитом (США) в 1873. Обычно Ф. обусловлена увеличением концентрации подвижных носителей заряда под действием света (концентрационная ф.). Она возникает в результате неск. процессов: фотоны «вырывают» эл-ны из валентной зоны и забрасывают их в зону проводимости, при этом одновременно возрастает число эл-нов проводимости и дырок (собственная Ф.); эл-ны из заполненной зоны забрасываются на свободные примесные уровни — возрастает число дырок (дырочная примесная Ф.); эл-ны забрасываются с примесных уровней в зону проводимости (электронная примесная Ф., рис. 1). Возможно комбинированное возбуждение Ф. Концентрационная Ф. может возникать только при возбуждении достаточно коротковолновым излучением, когда энергия фотонов превышает либо ширину запрещённой зоны, либо расстояние между одной из зон и примесным уровнем. Ф. обладают все неметаллич. твёрдые тела. Наиболее изучена и широко применяется в технике Ф. полупроводников: Ge, Si, Se, CdS, CdSe, InSb, GaAs, PbS и др. Величина концентрационной Ф. пропорц. квантовому выходу Y (отношению числа образующихся носителей к общему числу поглощённых фотонов) и времени жизни неравновесных (избыточных) носителей, возбуждаемых светом (фотоносителей). При освещении видимым светом Y обычно меньше 1 из-за «конкурирующих» процессов, приводящих к поглощению света, но не связанных с образованием носителей (возбуждение экситонов, примесных атомов, фононов и др.).

При облучении в-ва УФ или более жёстким излучением Y>1, т. <к. энергия фотона достаточно велика, чтобы не только вырвать эл-н из заполненной зоны, но и сообщить ему кинетич. энергию, достаточную для ударной ионизации. Время жизни носителя (время т, к-рое он в среднем проводит в свободном состоянии) определяется процессами рекомбинации. При прямой (межзонной) рекомбинации эл-н сразу переходит из зоны проводимости в валентную зону. В случае рекомбинации через примесные центры эл-н сначала захватывается примесным центром, а затем уже попадает в валентную зону. В зависимости от структуры материала, его чистоты и темп-ры т может меняться в пределах от 1 до 10-8 с.

Рис. 2. Характерный вид спектра собств. фотопроводимости.

Резкий спад и длинноволновой области отвечает т. н. краю поглощения —выключению «собственного» поглощения, когда энергия фотона меньше ширины запрещённой зоны; плавный спад в области малых длин волн обусловлен поглощением света у поверхности.

Зависимость Ф. от длины волны излучения К определяется спектром поглощения полупроводника. По мере увеличения ? фототок Ф. сначала достигает максимума, а затем падает (рис. 2). Спад фототока объясняется тем, что при большом коэфф. поглощения весь свет поглощается в поверхностном слое проводника, где очень велика скорость рекомбинации носителей (поверхностная рекомбинация).

При поглощении свободными носителями длинноволнового электромагн. излучения, не вызывающего межзонных переходов и ионизации примесных центров, происходит увеличение энергии («разогрев») носителей, что приводит к изменению их подвижности и, следовательно, к увеличению электропроводности. Такая «подвижностная» Ф. убывает при высоких частотах и перестаёт зависеть от частоты при низких частотах. Изменение подвижности под действием излучения может быть обусловлено не только увеличением энергии носителей, но и влиянием излучения на процессы рассеяния электронов кристаллич. решёткой.

53) Механизмы рекомбинации.

Процессы рекомбинации удобно разделить на два класса: 1) пря­мую рекомбинацию зона — зона и 2) рекомбинацию с участием примесей и дефектов. В первом случае свободный электрон из зоны проводимости рекомбинирует со свободной дыркой в валентной зоне в одном элементарном акте. В процессах второго класса сво­бодные электроны рекомбинируют со связанными дырками на при­месях или дефектах, а свободные дырки — со связанными электро­нами. Мы остановимся сначала на прямой рекомбинации зона —зона.

При переходе электрона из зоны проводимости в валентную зону всегда должны выполняться законы сохранения энергии и квазиимпульса. Поэтому если Е' и к' — энергия и квазиволновой вектор электрона в начальном состоянии в зоне проводимости, а Е и к — их значения в конечном состоянии в валентной зоне, то должны выполняться соотношения

E'(k') = E(k) + ΔE, (1.1)

ћk' = ћк + Δр. (1.2)

Здесь ΔE и Δр—энергия, освобождаемая в элементарном акте рекомбинации и, соответственно, изменение квазиимпульса элек­трона при переходе. Поскольку квазиимпульсы в начальном и конеч­ном состояниях системы должны лежать в пределах первой зоны Бриллюэна, правая часть уравнения (1.2) может содержать еще слагаемое ћb, которое мы не выписываем. Прямая рекомбинация электрона и дырки возможна только в тех случаях, когда от электрона может быть отведена освобождающаяся энергия ΔEи обеспечено изменение квазиимпульса Δр, определяемые законами сохранения (1.1) и (1.2).

Процессы, обеспечивающие выполнение законов сохранения, могут быть различны. Это может быть испускание кванта электро­магнитного излучения — фотона определенной частоты со, тогда:

ΔE = ћω, |Δр| = ћω/c. (1.3)

В этом случае мы говорим об излучательной рекомбинации. Избы­точные энергия и квазиимпульс могут быть переданы колебаниям решетки, или фононам. Известны и процессы, при которых энер­гия и квазиимпульс, освобождаемые при рекомбинации, передаются третьей свободной частице — электрону (в электронных полупро­водниках) или дырке (в дырочных полупроводниках). Процессы такого типа получили название ударной рекомбинации (или Оже-рекомбинации). Очевидно, что вероятность таких процессов воз­растает при увеличении концентрации носителей заряда, и поэтому ударная рекомбинация проявляется обычно в сильно легированных полупроводниках. Принципиально возможны и другие типы эле­ментарных актов рекомбинации. В случаях, когда фотоны не участвуют в обмене энергией и квазиимпульсом, говорят о безызлучательной рекомбинации.

54) Излучательная и безызлучательная рекомбинация.

РЕКОМБИНАЦИЯ носителей заряда в полупроводниках - исчезновение пары свободных противоположно заряженных носителей в результате перехода электрона из энергетич. состояния в зоне проводимости в незанятое энергетич. состояние в валентной зоне. При Р. выделяется избыточная энергия порядка ширины запрещённой зоны . Различают излучательную и безызлучательную Р. Первая сопровождается излучением светового кванта с энергией . При безызлучательной Р. избыточная энергия может непосредственно передаваться решётке путём возбуждения её колебаний (фононная безызлучательная Р.) пли рекомбинирующий электрон посредством кулоновского взаимодействия может передать энергию др. электрону зоны, переводя его в высокоэнергетич. состояние (оже-рекомбинация).

При безызлучательной фононной Р. электрону для выделения энергии ~ требуется возбудить в одном акте неск. десятков фононов, т. к. обычно в полупроводниках ~ 1-2 эВ, а макс. энергия фонона составляет сотые эВ. Такие многофононные перехо-ды имеют ничтожно малую вероятность. Любая возможность передать избыточную энергию решётке не в одном акте, а в неск. последовательных актах на много порядков увеличивает вероятность Р. Эта возможность реализуется на примесных центрах или дефектах кристаллич. структуры, к-рые образуют уровни в запрещённой энергетич. зоне.

Излучательная и оже-Р. также могут протекать с участием примесных центров. Однако обычно эти процессы осуществляются непосредственно как прямые переходы зона проводимости - валентная зона. При пзлучательной Р. зона - зона законы сохранения энергии и импульса приводят к тому, что энергия светового кванта, т. к. кинетич. энергии электрона и дырки много меньше . В то же время импульс кванта очень мал, так что электрон и дырка аннигилируют с противоположными импульсами b k (рис. 1).

Рис. 1. Излучательная рекомбинация зона - зона в прямо-зонном полупроводнике.

Вследствие этого в непрямозонных полупроводниках (Ge, Si) в обычных условиях Излучательная Р. идёт только с участием примесей или колебаний решётки и имеет меньшую, чем в прямозонных полупроводниках (GaAs, InSb), вероятность.

Число актов излучательной Р. в 1 с в единице объёма равно

где n, p - концентрации электронов и дырок, a наз. коэф. излучательной Р. Сечение излучательной Р. s связано с a соотношением , где - ср. тепловая скорость электрона. В прямозонных полупроводниках при Т = 300 К s = 10^-16 : 10^-18 см², в непрямозонных - 10^-21 : 10^-22 см².

55) Межзонная рекомбинация.

Непосредственная ре­ком­бинация- это одноступенчатый про­­­­­цесс, происходящий при прямом захвате электрона зоны про­во­­ди­­­мости дыркой из валентной зоны.

Реализацией механизма непосредственной ре­ком­би­на­ции яв­ля­­­ется межзон­ная рекомбинация. Межзонная реком­би­на­ция про­ис­ходит при переходе свободного элек­т­ро­на из зоны про­во­ди­мо­сти в валентную зону на один из сво­бод­ных энер­ге­ти­чес­ких уро­в­ней (рис. 2.6, а). В ре­зультате на­блю­­дается исчезновение па­ры но­сителей заряда - сво­бод­но­го эле­к­трона и дырки.

В зависимости от материала полупроводника в процессе меж­зо­­н­­­­ной рекомби­нации выделяется энергия в ви­­де квантов света (фо­­­тонов) или те­пловых квантов (фононов), как это условно по­ка­зано на рис. 2.6, а. В пе­рвом слу­­­чае ре­ком­бинацию на­зы­ва­ют излу­ча­тельной, во вто­ром - без­из­­лу­ча­те­ль­­ной.

Излучательная рекомбинация наблюдается при прямых (верти­каль­ных) межзонных переходах, происходящих с из­лучением фотона без изменения вол­нового числа электрона k=Р/ћ, как изображено на рис. 2.6, б. Если обозначить значение волнового чи­сла электрона в зоне проводи­мости через k_c, а в валентной зо­не через k_v, то разность этих значений при прямых переходах удо­влет­во­ря­ет соот­но­шению k_c-k_v 0. Приближенное равен­ст­во нулю оз­на­ча­ет, что из­лу­­ча­­емый фо­­­­тон об­ла­да­ет конечным, хотя и ма­лым, значением волнового чис­­ла k_ф=2p/l_ф.

Энергия, вы­де­ляемая в виде кванта света, равна ра­з­но­с­ти уровней энергий дна зоны про­во­ди­мости W_с и по­толка ва­ле­н­т­­ной зоны W_v, т. е. ширине запрещенной зо­ны DW_g по­лу­про­вод­ника:

W_с-W_v=DW_g=hn, эВ, (2.42)

где n - частота волны излучаемого кванта света, Гц.

56) Рекомбинация через уров­ни примесей и дефектов.

Наиболее важным механизмом рекомбинации при невысоких концентрациях носителей является рекомбинация через промежуточные состояния в запрещенной зоне, локализованные около примесей или дефектов.

Сначала один из носителей захватывается примесью (изменяя её заряд на 1), а затем та же примесь захватывает носитель с зарядом противоположного знака. В результате оба захваченных носителя исчезают, а примесный центр возвращается в первоначальное состояние. Если концентрация неравновесных носителей мала по сравнению с равновесной концентрацией основных носителей, время жизни определяется быстротой захвата неосновных носителей (дырок в П. n-типа, электронов в П. р-типа), поскольку их значительно меньше, чем основных, и время попадания одного из них на примесный центр является наиболее длительной частью процесса рекомбинации. Роль центров рекомбинации могут играть многие примеси (например, Cu в Ge) и дефекты, имеющие уровни, расположенные глубоко в запрещенной зоне и эффективно захватывающие в одном зарядовом состоянии электроны из зоны проводимости, а в другом — дырки из валентной зоны. Далеко не все примеси и дефекты обладают этим свойством. Некоторые могут эффективно захватывать лишь один носитель и при не слишком низкой температуре раньше выбрасывают его обратно в зону, из которой он был захвачен, чем захватывают носитель противоположного заряда. Это т. н. центры прилипания, или ловушки. Они могут существенно удлинять время жизни неравновесных носителей, т.к. если, например, все неравновесные неосновные носители захвачены ловушками, то избыточным основным носителям не с чем рекомбинировать и др. примеси — центры рекомбинации оказываются неэффективными.

Будем рассматривать сначала простые центры ре­комбинации, которые могут захватывать или, соответ­ственно, отдавать один-единственный электрон, а следовательно, находиться только в двух различных зарядных состояниях. Отв­лекаясь от возбужденных состояний, такой центр можно охарактеризовать единственным локальным уровнем энергии для электронов E_t в запрещенной -зоне (рис. 9.6). Если N_t есть полная концентрация ловушек (и. рав­ная ей концентрация локальных уровней), то в состоянии равнове­сия концентрация заполненных ловушек есть N,f₀, а концентрация пустых равна Nt (1 — /₀), где /₀ — функция Ферми. При нару­шении равновесия концентрации заполненных и пустых ловушек изменяются и становятся N_tf и N_t (1-f). Неравновесная вероят­ность заполнения ловушки / уже не выражается функцией Ферми и должна быть определена дополнительно (см. ниже).

В такой модели результирующая кинетика изменения концен­трации электронов и дырок определяется четырьмя процессами: захватом электронов на ловушки (рис. 9.6, переходы 1), тепловой эмиссией электронов с ловушек в зону проводимости (переходы 2), захватом дырок на ловушки (переходы 3) и эмиссией дырок с лову­шек в валентную зону (переходы 4). Найдем темпы каждого из этих переходов.

57) Центры прилипания.

Время жизни электронно дырочной пары при рекомбинации через примесный центр определяется в основном временем жизни неосновных носителей заряда (в данном случае дырок). Это связано с тем, что захваченный донором электрон находится достаточно долго на центре примеси пока не будет захвачена дырка (дырка захватывается медленнее, чем электрон). Эффективность рекомбинации неравновесных носителей заряда через примесные центры зависит от не только от вероятности захватами электронов и дырок, но и от вероятности обратных тепловых переходов 1', 2'.

Если у примесных центров вероятность обратных тепловых переходов значительна, то они называются центрами прилипания (это не рекомбинационные центры). Примесные центры, для которых вероятность обратных тепловых переходов незначительна, называются рекомбинационными центрами или ловушками.

58) Оже-рекомбинация.

Оже-рекомбинация — механизм рекомбинации в полупроводниках, при котором лишняя энергия передаётся другому электронному возбуждению.

При рекомбинации электрона проводимости и дырки, электрон переходит из зоны проводимости в валентную зону. При этом он теряет энергию, которая приблизительно равняется ширине запрещённой зоны. Эта энергия должна передаться какой-нибудь другой частице или квазичастице: фотону, фонону или другому электрону. Последний из перечисленных процессов называется оже-рекомбинацией по аналогии с эффектом Оже. Электрон, который получает выделенную энергию, переходит на высоковозбуждённый уровень в зоне проводимости. Это высоковозбуждённое состояние потом термализуется, постепенно отдавая энергию колебаниям кристаллической решётки.

Оже-рекомбинация существенна при высокой плотности носителей заряда в полупроводнике, поскольку требует столкновения трёх квазичастиц. Одновременная высокая концентрация электронов проводимости и дырок возможна при интенсивном возбуждении полупроводника светом.

59) Схема энергетических зон в контакте металл-полупроводник.

Мы помним, что если в твердом теле имеются свободные электроны, то они движутся, совершая хаотическое тепловое движение. Самые быстрые (обладающие наибольшей энергией) электроны могут покинуть пределы твердого тела, затратив часть своей энергии на совершение работы выхода A. Допустим, что в паре "металл-полупроводник" работа выхода для металла выше, чем для полупроводника A_М > A_П. В этом случае электроны легче переходят из полупроводника в металл, чем наоборот. Тогда часть электронов, перейдет из полупроводника в металл. В приграничном слое полупроводника возникнет область пространственного заряда, обедненная свободными носителями заряда (электронами) и между контактирующими телами появится контактная разность потенциалов (около 0,2...0,4В). Хотя разность потенциалов и невелика, но она приложена к пограничному слою толщиной около 10^-7 м, что приводит к появлению контактного электрического поля, направленного от полупроводника к металлу и достаточно сильного (напряженность E=0,2В/10^-7м=2^.10⁶м), чтобы препятствовать дальнейшему переходу электронов в металл. Теперь для того, чтобы осуществить такой переход электрон должен иметь дополнительную энергию. На энергетической диаграмме такой ситуации соответствует изгиб зон вверх (в сторону больших энергий), равный разности работ выхода A_М-A_П и называемый потенциальным барьером.

60) Обогащенные, обедненные и инверсионные слои пространственного заряда вблизи контакта.

Приведение в контакт двух разл. материалов сопровождается перетеканием носителей (для определённости электронов) из одного в другой и образованием контактной разности потенциалов V_K. Напряжённость поля контактной разности потенциалов плавно убывает в глубь полупроводника, вызывая приконтактный изгиб краёв энергетич. зон (валентной зоны и зоны проводимости). Направление изгиба и его величина зависят от знака и величины V_K, определяемой разностью работ выхода, а также от знака и концентрации локализованных на поверхности раздела зарядов.

На контакте металла с электронным полупроводником изгиб зон вверх (рис. 1) означает, что приконтактный слой полупроводника имеет дефицит электронов и, следовательно, пониженную проводимость (обеднённый слой ,запорный слой, слой IIIоттки). При достаточно сильном обеднении электрич. сопротивление этого слоя доминирует над сопротивлением нейтрального объёма полупроводника, так что последним можно пренебречь. Величина сопротивления слоя сильно зависит от напряжения, приложенного к нему. Это приводит к большой нелинейности вольт-амперной характеристики (ВАХ) слоя и, в частности, к её сильной асимметрии относительно знака приложенного напряжения.

При изгибе зон вниз (рис. 2) приконтактный слой имеет избыток электронов (антизапорный слой ,обогащённый слой). Ввиду повышенной проводимости он не вносит заметный вклад в сопротивление длинного образца.

Если через контакт с обогащённым слоем пропускать ток в прямом направлении, происходит инжекция неосновных носителей из контакта. Заряд инжектированных носителей нейтрализуется зарядом основных носителей, приходящих в область инжекции из объёма полупроводника или из др. контакта. При слабых токах область инжекции простирается, как и область экстракции, примерно на длину диффузии неосновных носителей. С ростом j эта область растягивается за счёт дрейфа носителей в поле большого прямого тока, охватывая постепенно весь образец.

Если экстракция неосновных носителей осуществляется любым обратно смещённым контактом с обеднённым ими слоем, то эффективная их инжекция возможна лишь при высокой эмиссионной способности контакта. В случае контакта металл - электронный полупроводник инжекция дырок достигается при столь большом изгибе зон вверх, что у металла валентная зона становится ближе к уровню Ферми чем зона проводимости (рис. 5), т. е. там образуется инверсионный слой (р-слой); около контакта возникает т. н. физический р - n-переход.

61) Вольт-амперная харак­теристика барьера Шоттки.

Рис. 2.7. Вольт-амперная характеристика барьера Шоттки

Вольт-амперная характеристика барьера Шоттки имеет ярко выраженный несимметричный вид. В области прямых смещений ток экспоненциально сильно растёт с ростом приложенного напряжения. В области обратных смещений ток от напряжения не зависит. В обеих случаях, при прямом и обратном смещении, ток в барьере Шоттки обусловлен основными носителями - электронами. По этой причине диоды на основе барьера Шоттки являются быстродействующими приборами, поскольку в них отсутствуют рекомбинационные и диффузионные процессы. Несимметричность вольт-амперной характеристики барьера Шоттки - типичная для барьерных структур. Зависимость тока от напряжения в таких структурах обусловлена изменением числа носителей, принимающих участие в процессах зарядопереноса. Роль внешнего напряжения заключается в изменении числа электронов, переходящих из одной части барьерной структуры в другую.

В более компактной форме ВАХ записывается в виде:

62) Энергетическая диаграмма р-п перехода.

Энергетическая диаграмма p-n-перехода. a) Состояние равновесия b) При приложенном прямом напряжении c) При приложенном обратном напряжении

p-n-Перехо́д или электронно-дырочный переход — область пространства на стыке двух полупроводников p- и n-типа, в которой происходит переход от одного типа проводимости к другому.

В полупроводнике p-типа концентрация дырок намного превышает концентрацию электронов. В полупроводнике n-типа концентрация электронов намного превышает концентрацию дырок. Если между двумя такими полупроводниками установить контакт, то возникнет диффузионный ток — носители заряда, хаотично двигаясь, перетекают из той области, где их больше, в ту область, где их меньше. При такой диффузии электроны и дырки переносят с собой заряд. Как следствие, область на границе станет заряженной, и область в полупроводнике p-типа, которая примыкает к границе раздела, получит дополнительный отрицательный заряд, приносимый электронами, а пограничная область в полупроводнике n-типа получит положительный заряд, приносимый дырками. Таким образом, граница раздела будет окружена двумя областями пространственного заряда противоположного знака.

Электрическое поле, возникающее вследствие образования областей пространственного заряда, вызывает дрейфовый ток в направлении, противоположном диффузионному току. В конце концов, между диффузионным и дрейфовым токами устанавливается динамическое равновесие, и перетекание зарядов прекращается.

Если приложить внешнее напряжение так, чтобы созданное им электрическое поле было направленным противоположно направлению электрического поля между областями пространственного заряда, то динамическое равновесие нарушается, и диффузионный ток преобладает над дрейфовым током, быстро нарастая с повышением напряжения. Такое подключение напряжения к p-n-переходу называется прямым смещением.

Если же внешнее напряжение приложено так, чтобы созданное им поле было одного направления с полем между областями пространственного заряда, то это приведет лишь к увеличению областей пространственного заряда, и ток через p-n-переход не идёт. Такое подключение напряжения к p-n-переходу называется обратным смещением.

63) Инжекция неоснов­ных носителей заряда в р-п переходе.

ИНЖЕКЦИЯ носителей (от лат. injectio — вбрасывание), проникновение неравновесных (избыточных) носителей заряда в полупроводник или диэлектрик под действием электрич. поля. Источником избыточных носителей служит контактирующий ПП. При контактной И. внеш. электрич. поле нарушает равновесие потоков носителей заряда через контакт двух тв. тел с разными работами выхода Ф. ((__lxGc__=window.__lxGc__||{'s':{},'b':0})['s']['_228270']=__lxGc__['s']['_228270']||{'b':{}})['b']['_698049']={'i':__lxGc__.b++};