
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
РАЗДЕЛ 1
СВОЙСТВА ЖИДКОСТИ
Плотность жидкости – параметр, характеризующий количество ее массы m в единице объема V,
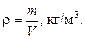 (1.1)
(1.1)
Плотность смеси разных веществ определяется выражением
 (1.2)
(1.2)
В табл.1.1 приведены значения плотности некоторых жидкостей и газов.
Таблица 1.1
| Жидкость | Температура, оС | Плотность, кг/м3 | Жидкость | Температура, оС | Плотность, кг/м3 |
| Метан | 0,668 | Мазут | - | 933-998 | |
| Воздух | 1,186 | Минеральные масла | - | 850-920 | |
| Воздух | 1,293 | ||||
| Керосин | 806-831 | Вода | |||
| Спирт | Глицерин | ||||
| Нефть | 850-950 | Ртуть |
Удельный вес – сила тяжести (вес) вещества в единице объема:
 Н/м3. (1.3)
Н/м3. (1.3)
Сжимаемость – свойство жидкости изменять свой объем V при изменении давления р. Сжимаемость характеризуется коэффициентом сжимаемостиaр (м2/Н) или модулем упругости жидкости Еж (Н/м2 = Па) (табл.1.2),
 (1.4)
(1.4)
При увеличении давления на величину Dр начальный объем жидкости V уменьшится на величину DV:
 (1.5)
(1.5)
Плотность этой жидкости изменится согласно зависимости
 (1.6)
(1.6)
где rо – начальная плотность жидкости при начальном давлении; rр – плотность при конечном давлении.
Таблица 1.2
| Жидкость | Среднее значение Еж, МПа | Жидкость | Среднее значение Еж, МПа |
| Спирт | Мин. масла | ||
| Керосин | Вода | ||
| Нефть | Глицерин |
Тепловое расширение – свойство жидкости изменять свой объем при изменении температуры. Тепловое расширение характеризуется коэффициентом объемного расширения at. При увеличении температуры на величину Dt начальный объем жидкости V увеличится:
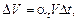 (1.7)
(1.7)
а плотность изменится в соответствии с формулой
 (1.8)
(1.8)
Среднее значение at для некоторых жидкостей при t = 20 °С дано в табл.1.3.
Таблица 1.3
| Жидкость | at, К-1 | Жидкость | at, К-1 |
| Вода | (1,5-2) 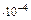
| Керосин | 9,6 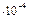
|
| Глицерин | 4,9 
| Спирт | 11 
|
| Минеральные масла | 7 
|
Величина at зависит от температуры и давления. Значения коэффициента at для воды при р = 0,1 МПа приведены в табл.1.4.
Таблица 1.4
| T, оС | 1-10 | 10-20 | 40-50 | 60-70 | 90-100 |
| at, К-1 | 
| 
| 
| 
| 
|
Совместное влияние давления и температуры на плотность жидкости можно примерно оценить зависимостью
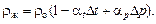 (1.9)
(1.9)
Вязкость – свойство жидкости оказывать сопротивление сдвигу ее слоев или их относительному смещению. Вязкость проявляется при движении жидкости, при этом возникают касательные напряжения t, которые пропорциональны (коэффициент пропорциональности m) градиенту скорости  , т.е.
, т.е.
 (1.10)
(1.10)
Коэффициент пропорциональности есть динамический коэффициент вязкости
 ,
,  , (1.11)
, (1.11)
где n – кинематический коэффициент вязкости, м2/с.
Иногда встречаются внесистемные единицы: для m – пуаз (П), для n – стокс (Ст). Соотношение между внесистемными единицами и единицами СИ:


В табл.1.5 приведены значения n для некоторых жидкостей.
Таблица 1.5
| Жидкость | Температура, оС | n×106, м2/с | Жидкость | Температура, оС | n×106, м2/с |
| Бензин | 0,60 | Масла минеральные (гидропривод) | 9,6-55 | ||
| Вода | 1,006 | ||||
| Спирт этиловый | 1,51 | Нефть | 25-140 | ||
| Керосин | 15-20 | 2-2,5 | Мазут топочный | 44-118 | |
| Воздух | 14,5 | Глицерин |
Кинематический коэффициент вязкости для воды в зависимости от температуры можно определить по эмпирической формуле
 м2/с. (1.12)
м2/с. (1.12)
В табл.1.6 приведены значения n воздуха и керосина для разных температур
Таблица 1.6
| Жидкость | n×106, м2/с | |||
| t = 0 °С | 15 °С | 18 °С | 20 °С | |
| Воздух | 14,5 | - | ||
| Керосин | - | - | 2,5 | 2,2 |
Вязкость также может быть представлена условными единицами (ВУ – вязкость условная) или градусами Энглера (°Е)
°Е = t/tо, (1.13)
где tо = 52 с – водное число, соответствующее времени истечения 200 см3 дистиллированной воды при 20 °С; t – время истечения из вискозиметра Энглера того же объема жидкости при заданной температуре.
Через градус Энглера (или ВУ) коэффициент n выражается следующим образом:
 м2/с. (1.14)
м2/с. (1.14)
Сведения о коэффициентах n и m также содержатся в справочной литературе [1].
В ряде случаев может быть задан закон изменения местной скорости в рассматриваемом сечении плоского потока, например, в виде  , где u и n – величины, входящие в градиент скорости
, где u и n – величины, входящие в градиент скорости  . Определять заданные параметры следует с использованием соответствующей производной при заданных граничных параметрах.
. Определять заданные параметры следует с использованием соответствующей производной при заданных граничных параметрах.
В других ситуациях возникает необходимость определять силы трения или момент сил трения при вращении одной детали относительно другой, если в кольцевом зазоре между ними находится какая-либо жидкость. Здесь сила трения определяется по формуле
 Н, (1.15)
Н, (1.15)
где D и b – соответственно диаметр и длина цапфы; s – зазор между перемещающимися поверхностями; uo – скорость движущейся поверхности.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1.1. Найти отношение удельных весов воды у поверхности Земли (g1) и на такой высоте от поверхности, где ускорение свободного падения g2 = 4 м/с2 (g2), если у поверхности плотность воды ρ = 1000 кг/м3.
Решение. У поверхности Земли g1 = 9,81 м/с2. Искомое соотношение согласно выражению (1.3)
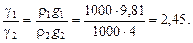
Ответ: 
Пример 1.2. При напорном течении горячего мазута по трубе касательное напряжение на ее внутренней поверхности составляет t = 2 Па. Найти значение кинематического коэффициента вязкости мазута, если скорость в поперечном сечении трубы изменяется согласно уравнению 
Решение. Согласно формуле (1.10)  , а с учетом формулы (1.11)
, а с учетом формулы (1.11)  ; y = n. Примем плотность мазута r = 933 кг/м3 (см. табл.1.1). Производная
; y = n. Примем плотность мазута r = 933 кг/м3 (см. табл.1.1). Производная  . На стенке трубы, где действует заданное напряжение t, у = 0; при этом
. На стенке трубы, где действует заданное напряжение t, у = 0; при этом  и искомый коэффициент
и искомый коэффициент  м2/с. Сравнение с данными табл.1.5 подтверждает правильность найденного решения.
м2/с. Сравнение с данными табл.1.5 подтверждает правильность найденного решения.
Ответ:n = 53,5×10-6 м2/с.
Пример 1.3. При гидроопрессовке баллона он был заполнен водой при давлении р1 = 6 МПа. В результате утечки части воды через неплотности давление в баллоне снизилось вдвое.
Пренебрегая деформацией стенок баллона, определить объем воды DV, вытекшей за время опрессовки, если диаметр баллона D = 350 мм, а его высота Н = 1200 мм.
Решение. Согласно формуле (1.5)  . По табл.1.2 для воды Еж = 2050 МПа. Изменение давления за время опрессовки
. По табл.1.2 для воды Еж = 2050 МПа. Изменение давления за время опрессовки  Объем воды в баллоне
Объем воды в баллоне  м3.
м3.
Искомая утечка:

Ответ: DV = 0,168 л.
ЗАДАЧИ
Задача 1.1.Определить, во сколько раз изменится плотность воздуха, если его нагреть от 0 до 80 °С при постоянном давлении.
Ответ: в 1,293 раза.
Задача 1.2.В резервуар, содержащий 125 м3 нефти плотностью 760 кг/м3, закачано 224 м3 нефти плотностью 848 кг/м3. Определить плотность смеси.
Ответ:rсм = 816,5 кг/м3.
Задача 1.3. Определить объем, занимаемый нефтью весом 1,25 МН, если ее плотность равна 850 кг/м3.
Ответ: V = 149,9 м3.
Задача 1.4.В резервуар залито 15 м3 нефти плотностью 800 кг/м3. Сколько необходимо долить нефти плотностью 824 кг/м3, чтобы плотность смеси стала равной 814 кг/м3?
Ответ: V2 = 21 м3.
Задача 1.5.В резервуар залито 20 м3 нефти плотностью 850 кг/м3 и 25 м3 нефти плотностью 840 кг/м3. Определить плотность смеси.
Ответ:rсм = 844,4 кг/м3.
Задача 1.6.Определить удельный вес жидкости при ускорении силы тяжести 9,81 м/с2 и 2 м/с2, если 0,8 л этой жидкости уравновешиваются гирей массой 1,5 кг.
Ответ:g1 = 18394 Н/м3; g2 = 3750 Н/м3.
Задача 1.7.Определить ориентировочно вид жидкости, если 11,9 л этой жидкости уравновешиваются гирей массой 15 кг на уровне поверхности моря.
Ответ: жидкость – глицерин.
Задача 1.8. Сосуд объемом 2 м3 заполнен водой. На сколько уменьшится и чему станет равным объем воды при увеличении давления на 2×107 Па?
Ответ:DV = 0,0195 м3; V2 = 1,9804 м3.
Задача 1.9.При давлении р1 = 0,1 МПа объем воды в баллоне составляет V. На сколько процентов сократится этот объем при увеличении давления в 50 раз?
Ответ:DV составляет 0,24 % от V.
Задача 1.10.Баллон объемом 36 дм3 заполнен нефтью и плотно закрыт при давлении 1×105 Па. Какое количество нефти необходимо закачать в баллон дополнительно, чтобы давление в нем повысилось в 25 раз? Деформацией стенок баллона пренебречь.
Ответ:DV = 65 см3.
Задача 1.11.При испытании резервуара гидравлическим способом он был заполнен водой при давлении 50×105 Па. В результате утечки части воды через неплотности давление в резервуаре понизилось до 11,5×105 Па. Пренебрегая деформацией стенок резервуара, определить объем воды, вытекшей за время испытания. Объем резервуара 20 м3.
Ответ:DV = 0,037 м3.
Задача 1.12.Определить давление, требующееся для сжатия жидкости с объемным модулем упругости Еж = 2000 МПа в 1,5 раза.
Ответ: р = 666 МПа.
Задача 1.13.Определить, во сколько раз сжимается жидкость с объемным модулем упругости Еж = 2100 МПа под давлением р = 200 МПа.
Ответ:в 1,11 раза.
Задача 1 14.Стальной горизонтальный трубопровод длиной L = 15 км, диаметром D = 0,6 м опрессовывают водой с давлением р = 0,6 МПа. Определить объем воды V, закачиваемый в трубопровод в процессе опрессовки. Упругостью стенок трубопровода пренебречь.
Ответ: V = 4240,24 м3.
Задач 1.15.Определить, какой вес должен иметь батискаф, чтобы достигнуть глубины Н = 1400 м при диаметре корпуса D = 3 м и длине L = 6 м. Плотность морской воды на поверхности составляет 1030 кг/м3, температура 20 °С. Температура воды на глубине 1400 м равна 4 °С. Коэффициент сжимаемости воды 0.49×10-9 Па-1, коэффициент теплового объемного расширения воды 1×10-4 К-1.
Ответ: G > 431975 Н.
Задача 1.16.23500 кг бензина при температуре 276 К занимают объем 33,25 м3. Какой объем будет занимать бензин при температуре 290 К, если давление не изменится? Коэффициент температурного расширения бензина принять at = 0,00065 К-1.
Ответ:33,56 м3.
Задача 1.17.Стальной баллон заполнен водой и плотно закрыт при t1 = 20 °С и давлении р1 = 0,1 МПа. Определить давление р2 в баллоне при t2 = 60 °С. При t = 20 °С плотность воды r20 = 998,23 кг/м3, а при t = 60 °С r60 = 983,24 кг/м3. Модуль упругости воды принять равным 2050 МПа.
Ответ: р2 = 30,89 МПа.
Задача 1.18.Определить динамический коэффициент вязкости жидкости и ее вид (ориентировочно), если при объеме V = 200 мл и весе G = 1,8 Н она вытекает из вискозиметра Энглера при водном числе tо = 52 с за время t = 208 с.
Ответ:m = 0,0257 Па×с; жидкость – минеральное масло.
Задача 1.19.Чему равен динамический коэффициент вязкости мазута, если его плотность 933 кг/м3, а вязкость составляет 8 °Е?
Ответ:m = 5,38×10-2 Па×с.
Задача 1.20.Каково будет касательное напряжение у внутренней стенки топливного трубопровода при перекачивании топлива с вязкостью 10 °Е и плотностью r = 932 кг/м3, если градиент скорости равен 4?
Ответ:t = 0,27 Па.
Задача 1.21.Определить касательное напряжение на поверхности движущегося судна, если изменение скорости воды u по нормали к этой поверхности выражается уравнением и = 516y – 13400y2, справедливым при значениях у < 1,93×10-2 м; температура воды равна 15 °С.
Ответ:t = 0,58 Па.
Задача 1.22.Какова сила трения на внутренней стенке топливного трубопровода диаметром D = 80 мм и длиной L = 10 м, если скорость движения топлива по сечению трубопровода изменяется по закону u = 25y – 312у2 (где у – расстояние от внутренней поверхности трубопровода, которое изменяется от 0 до 0,5D)? Вязкость топлива составляет 9 °Е, плотность топлива r = 920 кг/м3. Чему равна максимальная скорость движения топлива в трубопроводе?
Ответ: Т = 3,76 Н; umax = 0,5 м/с.
Задача 1.23.Определить силу Т поверхностного трения тонкой пластины длиной L = 3 м, шириной b = 1 м, обтекаемой с двух сторон водой при температуре t = 15 °С, если скорость воды вблизи поверхности пластины в направлении нормали к ней изменяется по уравнению u = 200y – 2500y2 (значения у изменяются от 0 до 0,04 м).
Ответ: Т = 1,37 Н.
Задача 1.24.Плотность нефти при температуре t = 280 К равна 850 кг/м3. Условная вязкость ее при температуре 295 К равна 6,4 °Е. Определить динамическую вязкость нефти при температуре 295 К, если коэффициент температурного расширения at = 0,72×10-3 К-1.
Ответ:m = 0,0385 Па×с.
Задача 1.25.При определении вискозиметром условной вязкости дизельного масла ДП-II при температуре 100 °С время истечения 200 см3 масла составило 1 мин 35,5 с. Водное число вискозиметра 50,3 с. Определить коэффициент кинематической вязкости масла.
Ответ:n = 10,56×10-6 м2/с.
Задача 1.26.Определить кинематический коэффициент вязкости минерального масла, если его удельный вес g = 8500 Н/м3, а динамический коэффициент вязкости m = 0,0986 Па×с.
Ответ:n = 114×10-6 м2/с.
Задача 1.27.Найти динамический коэффициент вязкости жидкости в зазоре s = 5 мм между двумя цилиндрами длиной L = 90 см, средним диаметром Dср = 40 см при числе оборотов внутреннего цилиндра n = 50 об/мин и силе, удерживающей наружный цилиндр Т = 3 Н.
Ответ:m = 0,0127 Па×с.

Дата добавления: 2015-04-18; просмотров: 509; Мы поможем в написании вашей работы!; Нарушение авторских прав |