
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
РАЗДЕЛ 5
ГИДРАВЛИЧЕСКИЙ РАСЧЕТ
НАПОРНЫХ ТРУБОПРОВОДОВ
В разделе рассматриваются длинные трубопроводы, последовательное и параллельное соединение простых трубопроводов, трубопроводы с путевой раздачей и распределительные сети (применительно к расчетно-графической работе).
В длинных трубопроводах влияние местных потерь энергии  или
или 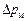 (см. раздел 3) невелико. Эти потери, как правило, учитывают, увеличив потери энергии по длине Dhl (или Dpl) на 10 %.
(см. раздел 3) невелико. Эти потери, как правило, учитывают, увеличив потери энергии по длине Dhl (или Dpl) на 10 %.
Потери энергии по длине определяются по формуле Дарси:
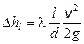 или
или  (5.1)
(5.1)
где l – коэффициент гидравлического трения (коэффициент Дарси); l – приведенная длина расчетного участка трубы, м; v – средняя скорость потока, м/с; d – диаметр трубы, м; r – плотность жидкости, кг/м3.
Формулу (5.1) можно привести к таким выражениям:
 ; (5.2)
; (5.2)
 ; (5.3)
; (5.3)
 , (5.4)
, (5.4)
где Q – объемный расход, м3/с; А – удельное сопротивление трубопровода, с2/м6; K – расходная характеристика, м3/с; а – полное сопротивление трубопровода, с2/м5; i – гидравлический уклон;
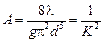 ; (5.5)
; (5.5)
 ; (5.6)
; (5.6)
 . (5.7)
. (5.7)
Для длинных трубопроводов можно пренебречь кинетической составляющей уравнения Бернулли (3.12), так как 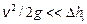 . Тогда разность пьезометрических высот в рассматриваемых сечениях трубопровода будет примерно равна потерям энергии
. Тогда разность пьезометрических высот в рассматриваемых сечениях трубопровода будет примерно равна потерям энергии 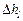 , т.е.
, т.е.
 . (5.8)
. (5.8)
Параметры А, K и a не зависят от числа Рейнольдса Re, если трубопровод работает в области квадратичного закона сопротивления, но зависят от диаметра трубы d и шероховатости ее стенок Dэ.
В табл.5.1 даны значения K4 (четвертая зона) для стальных труб при Dэ = 0,02 мм (новые трубы) и Dэ = 0,2 мм (трубы после нескольких лет эксплуатации или старые), а также для чугунных труб при Dэ = 0,2 мм (новые) и Dэ = 1 мм (старые); коэффициент Дарси l при этом определяется формулой (3.21).
Таблица 5.1
| d, мм | Расходная характеристика K4, л/с | |||
| Трубы стальные | Трубы чугунные | |||
| Новые | Старые | Новые | Старые | |
| 15,2 | 11,4 | 11,4 | 9,3 | |
| 44,4 | 33,3 | 33,3 | 27,2 | |
| 96,1 | 72,0 | 72,0 | 58,9 | |
| 172,4 | 129,5 | 129,5 | 105,9 | |
| 278,9 | 209,0 | 209,0 | 170,9 | |
| 593,0 | 444,3 | 444,3 | 364,0 | |
| 798,8 | 798,8 | 652,8 | ||
Часто трубопроводы работают не в квадратичной области сопротивления. Установить область можно, зная число Рейнольдса Re, диаметр d и шероховатость Dэ трубы по следующей ориентировочной цепочке соотношений (см. раздел 3):
0…I…2320…II…10  …III…500
…III…500  IV (5.9)
IV (5.9)
Область 0 <Re  2320 соответствует ламинарному режиму (первая зона). Потери энергии
2320 соответствует ламинарному режиму (первая зона). Потери энергии
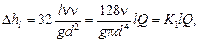 (5.10)
(5.10)
где n – кинематическая вязкость, м2/с; v – средняя скорость потока, м/с; l – длина рассматриваемого участка трубопровода, м; Q – объемный расход, м3/с;  – постоянная для ламинарного режима, с/м3.
– постоянная для ламинарного режима, с/м3.
Область II соответствует зоне гидравлически гладких труб; область III – зоне гидравлически шероховатых труб; область IV – квадратичная.
В общем случае для турбулентного движения рекомендуется формула А.Д.Альтшуля:

Убедившись на основании анализа цепочки (5.9), что рассматриваемый трубопровод работает не в квадратичной зоне, следует ввести на потери энергии (5.2) поправку y > 1
 , (5.11)
, (5.11)
где
m = 1+  , (5.12)
, (5.12)
или уменьшить модуль расхода K4 (табл.5.1) в соответствии с формулой
K3 = K4m-0,125 (5.13)
Простой трубопровод имеет постоянный диаметр d по всей длине l и не имеет ответвлений.
Для последовательного соединения простых трубопроводов полную потерю напора (энергии) определяют по формуле
 (5.14)
(5.14)
Потери напора на каждом участке определяются формулой (5.2).
При параллельном соединении простых трубопроводов потери напора в отдельных ветвях равны, т.е.  и т.д., а расходы Qi распределяются по отдельным ветвям согласно зависимости
и т.д., а расходы Qi распределяются по отдельным ветвям согласно зависимости
 . (5.15)
. (5.15)
Когда жидкость расходуется из трубопровода во многих его точках (путевой расход или непрерывная раздача), потеря напора определяется формулой
 (5.16)
(5.16)
где Q0 – начальный расход, непрерывно и равномерно расходуемый по длине трубы.
Если часть расхода проходит по трубе транзитом Qтр, а часть непрерывно расходуется по длине трубы Q0, то общая потеря напора
 ; Q = Qтр + Q0. (5.17)
; Q = Qтр + Q0. (5.17)
Объяснение структуры и сути распределительных сетей производится на примере порядка расчета сети для расчетно-графической работы (РГР).
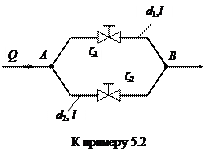
На рис.5.1 дан пример распределительной сети.

|
В соответствии с заданием (см. задачу 5.14. и табл.5.2) в пределах РГР необходимо:
· построить в масштабе по координатам l (длина) и z (геодезическая отметка) профиль трассы;
· определить диаметры участков трубопровода, рассчитать пьезометрические (Н) и рабочие (hр) напоры в заданных точках сети и построить пьезометрическую линию (ПЛ). Ось ординат должна быть общая для z, Н и hр;
· определить высоту установки насоса над уровнем воды в зумпфе (высоту всасывания zн) и мощность Nдв на валу центробежного насоса (мощность приводного двигателя).
Задано:
· узловые расходы Q2, Q3, Q4, Q5, Q6;
· геодезические отметки пунктов потребления z2, z3, z4, z5, z6;
· приведенные длины участков, учитывающие находящиеся на них местные сопротивления l12, l23, l34, l35, l26;
· рабочий напор hзад, ниже которого не может быть фактический, полученный расчетом рабочий напор hр (hзад задается преподавателем дополнительно);
· коэффициент полезного действия (КПД) насоса  ;
;
· частота вращения рабочего колеса насоса n, об/мин;
· вид труб (табл.5.1). Задается преподавателем дополнительно.
Выбор магистрали. В магистраль должны входить последовательно соединенные участки простых трубопроводов, образующие наиболее нагруженную по расходу и наиболее протяженную линию.
Согласно рис.5.1 в магистраль входят участки 0-1 и 1-2, далее необходимо сравнить между собой направления 2-6, 2-3-4 и 2-3-5.
Пусть в рассматриваемом примере (SQ)max и  относятся к направлению 2-3-5. Тогда магистралью является сеть из участков: 0-1, 1-2, 2-3, 3-5. Участки 2-6 и 3-4, не вошедшие в магистраль, являются ветвями.
относятся к направлению 2-3-5. Тогда магистралью является сеть из участков: 0-1, 1-2, 2-3, 3-5. Участки 2-6 и 3-4, не вошедшие в магистраль, являются ветвями.
Расчет магистрали следует начинать с наиболее удаленного от насоса участка, которым в примере является участок 3-5, и далее рассчитывать участки последовательно против потока (2-3; 1-2; 0-1).
Определить транзитные расходы на участках:
Q3-5 = Q5; Q3-4 = Q4; Q2-6 = Q6; Q2-3 = Q3 + Q4 + Q5;
Q0-1 ≈ Q1-2 = Q2 + Q3 + Q4 + Q5 + Q6.
Расчет последнего участка магистрали (уч. 3-5). Предварительно определить диаметр  , используя рекомендацию об ориентировочных скоростях жидкости: при Q = 6-50 л/с vпр = 0,7-1,0 м/с; при Q = 50-120 л/с vпр = 1,0-1,4 м/с;
, используя рекомендацию об ориентировочных скоростях жидкости: при Q = 6-50 л/с vпр = 0,7-1,0 м/с; при Q = 50-120 л/с vпр = 1,0-1,4 м/с;
 (5.18)
(5.18)
Далее по табл.5.1 следует выбрать ближайшее к  значение
значение 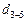 и соответствующий ему модуль расхода
и соответствующий ему модуль расхода  для заданного вида труб, который до уточнения является приблизительной величиной. Определить фактическую скорость жидкости на данном участке
для заданного вида труб, который до уточнения является приблизительной величиной. Определить фактическую скорость жидкости на данном участке
 (5.19)
(5.19)
Определить число Рейнольдса по выражению (3.16) и вязкость (1.12) для воды.
Установить фактическую область сопротивления, используя рекомендации к цепочке (5.9). Если  , найденный по табл.5.1 модуль расхода
, найденный по табл.5.1 модуль расхода  должен быть принят для дальнейших расчетов. Если
должен быть принят для дальнейших расчетов. Если  , следует определить поправку m по формуле (5.12) и откорректировать
, следует определить поправку m по формуле (5.12) и откорректировать  по формуле (5.13). Получим фактический модуль
по формуле (5.13). Получим фактический модуль  .
.
Определить потери напора на участке 3-5 Dh3-5 используя выражение (5.2).
Определить полный гидростатический напор в конце участка
Н5 = z5 + hзад; (5.20)
в начале участка
Н3 = Н5 + Dh3-5. (5.21)
Определить рабочий напор в начале участка
hр.3 = Н3 – z3 (5.22)
и сравнить его с hзад. Если hр.3 ³ hзад, приступить к построению пьезометрической линии (ПЛ) по точкам Н5 и Н3 и далее – к расчету следующего участка магистрали (2-3) по изложенной методике.
При расчете последнего участка магистрали и ветви в пояснительную записку внести все пояснения к расчетным параметрам и формулам. При расчете остальных участков магистрали пояснения можно опустить.
Если hр.3 < hзад, следует определить величину недостающего напора
 (5.23)
(5.23)
и на величину d поднять напоры в точках 3 и 5, после чего откорректировать ПЛ для участка 3-5. При этом рабочий напор hр.3 будет равен заданному hзад, а напор hр.5 будет больше заданного. Точки Н5 и Н3 соединить на графике прямой линией.
Расчет ветви. Для примера примем ветвь 3-4.
Определить предварительно полный гидростатический напор в конце ветви (точка 4)
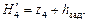 (5.24)
(5.24)
Значение аналогичного напора в начале ветви Н3 было определено при расчете магистрали (5.21).
Диаметр труб на участке 3-4 (d3-4) определяется по величине допустимой потери напора в ветви [Dh3-4] следующим образом:
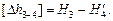 (5.25)
(5.25)
Определить предварительное значение модуля расхода
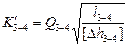 . (5.26)
. (5.26)
Далее по табл.5.1 следует найти для заданного вида труб ближайшее к  большее значение модуля. Этому значению K соответствует значение искомого диаметра d3-4.
большее значение модуля. Этому значению K соответствует значение искомого диаметра d3-4.
Определить фактическую скорость жидкости v3-4, используя (5.19); определить критерий Re (3.16), установить фактическую область сопротивления (5.9). Если  , найденный по табл.5.1 модуль
, найденный по табл.5.1 модуль  принимается для дальнейших расчетов. Если
принимается для дальнейших расчетов. Если  , следует определить поправку m (5.12) и откорректировать
, следует определить поправку m (5.12) и откорректировать  (5.13); получим фактический модуль
(5.13); получим фактический модуль  .
.
Определить фактическую потерю напора Dd3-4 по (5.2).
Сравнить Dh3-4 с [Dh3-4]. Если Dh3-4 < [Dh3-4], приступить к определению гидростатического напора Н4 =  и построению ПЛ для участка 3-4. Если Dh3-4 > [Dh3-4], следует вернуться к табл.5.1 методики и выбрать следующее большее значение модуля
и построению ПЛ для участка 3-4. Если Dh3-4 > [Dh3-4], следует вернуться к табл.5.1 методики и выбрать следующее большее значение модуля  . Для
. Для  найти по табл. 5.1 новый d3-4, который будет больше ранее выбранного.
найти по табл. 5.1 новый d3-4, который будет больше ранее выбранного.
Повторить действия после формулы (5.26); найти новое значение потерь напора Dh3-4, которое снова сравнить с [Dh3-4].
Определить фактический напор в точке 4
Н4 = Н3 – Dh3-4; (5.27)
найти рабочий напор в точке 4 hр.4 по (5.22).
Сравнить hр.4 c hзад. Если hр.4 < hзад, следует определить d (5.23) и поднять Н3, Н4 и Н5 на эту величину, при этом скорректировав ПЛ.
Определение приводной мощности насоса. Мощность приводного двигателя (или мощность на валу насоса) определяется по формуле
 (5.28)
(5.28)
где Нн – напор, создаваемый насосом; hн – КПД насоса;
 (5.29)
(5.29)
Н1 – напор на выходе из насоса, определен при расчете участка 1-2 магистрали; z – суммарный коэффициент местных сопротивлений во всасывающей линии 0-1, задан в табл. 5.2; 0-1 – индексация параметров всасывающей линии 0-1; Zн – предельно допустимая высота всасывания насоса по условиям его бескавитационной работы (для РГР – высота установки насоса над уровнем воды в зумпфе),
 (5.30)
(5.30)
pа – атмосферное давление; pнп – давление насыщенных паров [1];  – потери напора по длине всасывающего трубопровода (5.2); Dhм0-1– местные потери напора (3.22); v0-1 – средняя скорость жидкости во всасывающем трубопроводе;
– потери напора по длине всасывающего трубопровода (5.2); Dhм0-1– местные потери напора (3.22); v0-1 – средняя скорость жидкости во всасывающем трубопроводе;  – допустимый кавитационный запас,
– допустимый кавитационный запас,
 (5.31)
(5.31)
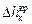 – критический кавитационный запас, определяется по формуле С.С.Руднева,
– критический кавитационный запас, определяется по формуле С.С.Руднева,
 (5.32)
(5.32)
С – кавитационный коэффициент, зависящий от конструктивных особенностей насоса, принять С = 1000.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 5.1. Определить напор в точке В (НВ) и расход в точке С (QC) горизонтального трубопровода (трубы стальные, старые), если трубопровод состоит из двух последовательно соединенных участков (АВ и ВС) с размерами: dAB = 100 мм, dBC = 75 мм, lAB = 470 м, lBC = 365 м.
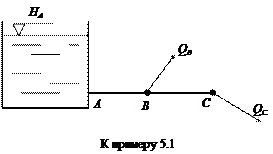
|
Известны также пьезометрические напоры НА = 28 м, НС = = 19 м и сосредоточенный расход QB = 3 л/с.
Решение. Для решения следует составить систему двух уравнений вида (5.2) для участков АВ и ВС с двумя неизвестными QС и НВ.
Потери напора на участке АВ
 ; (5.33)
; (5.33)
на участке ВС
 . (5.34)
. (5.34)
Из уравнения (5.34) найдем НВ и подставим в уравнение (5.33); при этом заменим  через аi по формуле (5.7):
через аi по формуле (5.7):

Отcюда
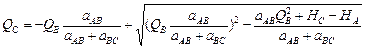 . (5.35)
. (5.35)
В задаче не указана область сопротивления, поэтому в первом приближении примем модуль расхода K из табл.5.1 для квадратичной области:
dАВ = 100 мм; 
dВС = 75 мм; 
Вычислим полное сопротивление (5.7)

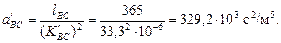
После подстановки в (5.35) известных составляющих получим
 .
.
Проверим область сопротивления по цепочке (5.9); при этом примем кинематическую вязкость воды 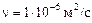 при t = 20 °С
при t = 20 °С


Для квадратичной зоны 
 ; фактически ReAB < 250000, следовательно, необходимо ввести на модуль расхода уменьшающую поправку m (5.12) и уточнить KАВ по формуле (5.13)
; фактически ReAB < 250000, следовательно, необходимо ввести на модуль расхода уменьшающую поправку m (5.12) и уточнить KАВ по формуле (5.13)
 ;
;

При этом 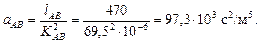
Аналогичные вычисления выполним для aBC:


500 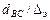 = 500
= 500  187500.
187500.
Так как ReBC < 187500, следует ввести поправку:



Подставив новые данные в формулу (5.35), получим:  При этом напор в точке В по формуле (5.34):
При этом напор в точке В по формуле (5.34):
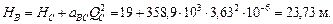
Ответ: QC = 3,63 л/с; НВ = 23,73 м.
|
Пример 5.2. Определить диаметры d1 и d2 труб при их параллельном соединении, если длины их одинаковы l1 = l2 = l = 1000 м, расходы воды составляют Q1 = 19,9 л/с, Q2 = 75,3 м3/с, а линейные потери напора от А до В Dh = 5,1 м.
Принять: трубу 1 стальную новую с Dэ.1 = 0,02 мм, трубу 2 чугунную старую с Dэ.2 = 1 мм; на трубе 1 установить шиберную задвижку с z1 = 40, на трубе 2 – задвижку с z1 = 15; плотность воды r = 1000 кг/м3, кинематическая вязкость n = 1×10-6 м2/с при t = 20 °С.
Решение. Определим расходную характеристику  приближенно считая, что потери энергии соответствуют только потерям по длине, т.е. линейным, а трубопроводы работают в квадратичной области сопротивления.
приближенно считая, что потери энергии соответствуют только потерям по длине, т.е. линейным, а трубопроводы работают в квадратичной области сопротивления.
Из формулы (5.2):
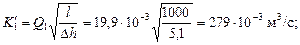
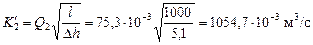 .
.
По табл.5.1 находим предварительные значения исходных диаметров:  = 150 мм и
= 150 мм и  = 300 мм.
= 300 мм.
Далее следует установить фактическую область сопротивления (5.9), в которой работают трубы, и при отклонении от квадратичности ввести для  поправку (5.13), а также учесть местные сопротивления, выразив их через эквивалентную длину
поправку (5.13), а также учесть местные сопротивления, выразив их через эквивалентную длину  :
:
 (5.36)
(5.36)

Средние скорости потока на участках:


Числа Рейнольдса:
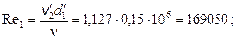

Область сопротивления:
· для  :
:  следовательно, данная труба работает не в квадратичной области сопротивления, и K1 <
следовательно, данная труба работает не в квадратичной области сопротивления, и K1 <  ;
;
· для  :
:  следовательно, данная труба работает в квадратичной области сопротивления, и K2 =
следовательно, данная труба работает в квадратичной области сопротивления, и K2 =  .
.
Определим для трубы 1 поправку на неквадратичность (5.12):
 m2 » 1.
m2 » 1.
Фактическая расходная характеристика с учетом области сопротивления и местных сопротивлений:

По табл.5.1 для K1 = 593,7 л/с находим d1 = 200 мм;

По табл.5.1 для K2 = 1141 л/с нет точного значения d2, но известно, что  < d2 < 350 мм. Более точное значение d2 можно получить по справочникам, содержащим d, Dэ и K, или вычислив d2, исходя из (3.21) и (5.6):
< d2 < 350 мм. Более точное значение d2 можно получить по справочникам, содержащим d, Dэ и K, или вычислив d2, исходя из (3.21) и (5.6):


Приравнивая эти выражения, находим фактическое значение d2 = 309 мм.
Ответ: d1 = 200 мм; d2 = 309 мм.
ЗАДАЧИ
Задача 5.1.Резервуар объемом V = 12,6 м3 требуется наполнить водой за время t = 30 мин. Определить расходную характеристику K и диаметр d водопроводной загрязненной трубы, по которой подается вода в резервуар, если ее шероховатость Dэ = 2 мм, длина l = 150 м и располагаемый напор в начале трубы Н = 2,6 м.
Проверка области сопротивления обязательна.
Ответ: K = 53 л/с; d = 100 мм.
Задача 5.2. Из бака А с горизонтом воды на отметке Ñ1 = 31 м в бак Б поступает расход Q = 25,8 л/с по трубопроводу приведенной длины l = 1520 м и диаметром d = 200 мм. Определить отметку Ñ2 в баке Б для двух вариантов:
а) трубы стальные, новые;
б) трубы чугунные, бывшие в употреблении.
Ответ: а) Ñ2 = 26,7 м; б) Ñ2 = 23,4 м.
Задача 5.3. Для условий задачи 5.2 определить расход Q и область сопротивления для двух вариантов:
а) отметка Ñ2 = 26,7 м, трубы чугунные новые;
б) отметка Ñ2 = 23,4 м, трубы стальные новые.
Использовать формулу (5.1) и способ последовательных приближений.
Ответ: а) Q = 22,6 л/с, переходная область; б) Q = 35 л/с, переходная область.

|
Задача 5.4. Горизонтальный трубопровод общей длиной L = 760 м пропускает из резервуара А в резервуар Б воду с расходом Q = 18,2 л/с. Трубопровод состоит из двух участков: первый – труба чугунная, бывшая в употреблении; второй – труба стальная, бывшая в употреблении.
Требуется подобрать диаметры этих труб d1, d2 и их длины l1, l2, если отметки уровней воды в резервуарах Ñ1 = +28 м, Ñ2 = +15 м.
В данной задаче множество решений. Чтобы сузить область решений, можно, используя данные табл.5.1, определить диапазон диаметров d, предположив, что трубопровод цельный, но представлен в одном случае чугунной трубой, а в другом – стальной.
Ответ: Один из возможных вариантов соответствует d1 = 0,15 м, l1 = 295,5 м и d2 = 0,125 м, l2 = 464,5 м.
Задача 5.5.Из резервуара под напором Н = 15,4 м вода поступает по трубам в водозаборные пункты А и В соответственно с расходом QА = 19 л/с и QВ = 38 л/с. Определить рабочие (пьезометрические) напоры в пунктах А и В (hр.A и hр.B), если:

|
· к пункту А проложена чугунная труба (бывшая в употреблении) диаметром d1 = 150 мм и длиной l1 = 432 м;
· к пункту В проложена новая стальная труба (d2 = 200 мм, l2 = 610 м).
Ответ: hр.A = 10,06 м; hр.B = 11,9 м.
Задача 5.6. Для условий задачи 5.5 определить пьезометрические напоры в пунктах А и В, если:
· к пункту А проложена новая стальная труба; d1 = 150 мм, l1 = 432 м;

|
· к пункту В проложена чугунная труба, бывшая в употреблении; d2 = 200 мм, l2= 610 м.
Ответ: hр.A = 12,73 м; hр.B = 8,75 м.
Задача 5.7.Вода с расходом Q = 18,3 л/с поступает из резервуара А в резервуар В по трубопроводу, составленному из трех последовательно соединенных участков стальных труб, бывших в употреблении, со следующими размерами:
| Участок А – 1 | Участок 1 – 2 | Участок 2 – В | |
| Диаметр d, мм | |||
| Длина l, м |
Определить отметку горизонта воды в резервуаре А (НА) и пьезометрические напоры в узлах 1 и 2.
Местными сопротивлениями пренебречь. Проверка области сопротивления обязательна.
Ответ: НА = 25,18 м; Н1 = 24,09 м; Н2 = 20,30 м.

|
Задача 5.8.В резервуар А из резервуара В поступает расход Q = 160 л/с по трем стальным трубопроводам (бывшим в употреблении) размерами: d1 = 0,2 м, l1 = 815 м; d2 = 0,15 м, l2 = 510 м; d3 = 0,1 м, l3 = 436 м.
Определить начальную отметку уровня воды в резервуаре В (НВ) и расходы Q1, Q2, Q3.
После определения расходов проверить область гидравлического сопротивления для труб 1, 2 и 3.
Ответ: НВ = 46,5 м; Q1 = 88 л/с; Q2 = 52,4 л/с; Q3 = 19,5 л/с.

|
Задача 5.9.Вода поступает из резервуара к потребителям на участке ВС с непрерывной раздачей.
Определить потери напора DhAC = Н при расходе воды Q = 12 л/с, диаметре трубопровода d = 0,125 м и длинах участков: lАВ = 510 м, lВС = 340 м, трубы представлены в двух вариантах:
а) трубы чугунные, бывшие в употреблении;
б) трубы стальные, бывшие в употреблении.
Ответ: На = 8 м; Нб = 5,8 м.
Задача 5.10.По системе горизонтальных трубопроводов одинакового сечения при открытии задвижки 4 подают жидкость в резервуары 1, 2 и 3 одинаковой вместимостью V. После достижения в одном из резервуаров объема V задвижку 4 закрывают.
Определить объем жидкости в каждом из двух других резервуаров, если режим движения жидкости во всех трубопроводах ламинарный.
Потери энергии в местных сопротивлениях и объем жидкости в трубах не учитывать.
Ответ: V3 = V; V2 =  V; V1 =
V; V1 = 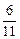 V.
V.

|
Задача 5.11. Для условий задачи 5.10 определить, в каких трубопроводах необходимо установить дополнительные местные сопротивления и какой эквивалентной длины lэ, чтобы резервуары заполнились одновременно.
Ответ: 1) дополнительные местные сопротивления следует установить в трубопроводах С – 3 и В – 2. 2) lэ.С–3 = 2l; lэ.B–2 = l.
Задача 5.12. Трубопровод чугунный, бывший в употреблении, имеет параллельное ответвление на участке ВС.
Таблица 5.2
| Номер варианта | Участковые расходы, л/с | Длины участков, м | Геодезические отметки, м | Коэффициент местных сопротивлений z0-1 | Частота вращения насоса n, об/мин | КПД насоса, hн | |||||||||||||||
| Q2 | Q3 | Q4 | Q5 | Q6 | l0-1 | l1-2 | l2-3 | l3-4 | l4-5 | l2-6 | z2 | z3 | z4 | z5 | z6 | ||||||
| 0,7 | |||||||||||||||||||||
| 0,69 | |||||||||||||||||||||
| 0,68 | |||||||||||||||||||||
| 0,66 | |||||||||||||||||||||
| 0,65 | |||||||||||||||||||||
| 0,66 | |||||||||||||||||||||
| 0,67 | |||||||||||||||||||||
| 0,68 | |||||||||||||||||||||
| 0,69 | |||||||||||||||||||||
| 0,70 | |||||||||||||||||||||
| 0,65 | |||||||||||||||||||||
| 0,66 | |||||||||||||||||||||
| 0,67 | |||||||||||||||||||||
| 0,68 | |||||||||||||||||||||
| 0,69 | |||||||||||||||||||||
| 0,7 | |||||||||||||||||||||

| |||||||||||||||||||||
| Окончание табл. 5.2 | |||||||||||||||||||||
| Номер варианта | Участковые расходы, л/с | Длины участков, м | Геодезические отметки, м | Коэффициент местных сопротивлений z0-1 | Частота вращения насоса n, об/мин | КПД насоса, hн | |||||||||||||||
| Q2 | Q3 | Q4 | Q5 | Q6 | l0-1 | l1-2 | l2-3 | l3-4 | l4-5 | l2-6 | z2 | z3 | z4 | z5 | z6 | ||||||
| 0,71 | |||||||||||||||||||||
| 0,72 | |||||||||||||||||||||
| 0,73 | |||||||||||||||||||||
| 0,74 | |||||||||||||||||||||
| 0,75 | |||||||||||||||||||||
| 0,74 | |||||||||||||||||||||
| 0,73 | |||||||||||||||||||||
| 0,72 | |||||||||||||||||||||
| 0,71 | |||||||||||||||||||||
Определить давление рн, развиваемое насосом для прокачки по трубопроводу воды с расходом Q = 80×10-3 м3/с, если в конце трубопровода (точка Д) свободный напор должен составлять НД = 20 м.
Размеры труб на участках:
| Участок АВ | Участок BmC | Участок ВС | Участок СД |
| l1 = 250 м | l2 = 200 м | l3 = 150 м | l4 = 300 м |
| d1 = 300 мм | d2 = 250 мм | d3 = 200 мм | d4 = 250 мм |
Проверка области сопротивления обязательна.
Ответ: рн = 0,27 МПа.
Задача 5.13. Решить задачу 5.12 для новых чугунных труб, если суммарный расход составляет Q = 160 л/с. Определение области сопротивления обязательно.
Ответ: рн = 0,38 МПа.
Задача 5.14.Для одного из указанных в табл.5.2 варианта условий построить профиль трассы трубопроводов распределительной сети и пьезометрическую линию, а также определить высоту установки насоса Zн и приводную мощность насоса Nпр.
Дата добавления: 2015-04-18; просмотров: 388; Мы поможем в написании вашей работы!; Нарушение авторских прав |