ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 4.1. В теле железобетонной плотины проектируются два водоспуска диаметром d и длиной L = 6 м. Уровень воды перед верхним водоспуском H₁ = 6,5 м. Истечение в атмосферу.

Определить диаметр d для пропуска через верхний водоспуск расхода Q₁ = 12 м³/с, а также максимально допустимое заглубление H₂ нижнего водоспуска из условий пропуска максимального расхода Q₂. Определить Q₂.

Решение. До определения диаметра d неясно – водоспуск является «насадком цилиндрическим наружным» или «короткой трубой». Для насадка при l/d = 3-4

, (4.2)

где m_н – коэффициент расхода.

При 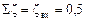и ll/d ® 0 m_н » 0,82 (табл.4.1). Для короткой трубы при l/d > 4 формулу (4.31) использовать нельзя, так как m_тр и S_тр зависят от искомого диаметра.

Найдем диаметр, предположив, что водоспуск – насадок,

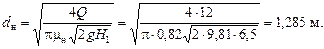
При этом т.е. водоспуск – скорее труба, чем насадок.

Найдем выражение для определения диаметра трубы d_т, для чего составим уравнение Бернулли для сечений 1-1 и 2-2, проведя плоскость сравнения 0-0 через ось трубы:

где z₁ = H₁; p₁ = p_a; v₁ » 0; z₂ = 0; p₂ = p_a; v₂ = v_т; v_т – скорость воды в трубе; ; .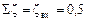

Выразим v_т через расход Q по формуле 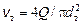. Тогда уравнение Бернулли примет вид:

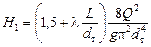. (4.32)

Примем в первом приближении, что движение воды по трубе соответствует квадратичной области сопротивления, т.е. 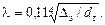Для бетонной трубы D_э = 0,5 мм (см. табл.3.1); тогда .

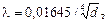После подстановки в формулу (4.32) H₁ = 6,5 м, 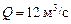, L = 6 м получим выражение

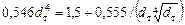. (4.33)

Решаем (4.33) способом последовательных приближений, приняв за первый шаг d_т = d_н = 1,285 м. Находим d_т = 1,361 м (1361 мм) > d_н. При этом 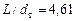, что соответствует понятию «короткая труба»; l = 0,0152.

Коэффициент расхода

;

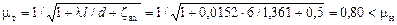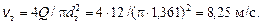
Таким образом, (квадратичная область сопротивления, формула выбрана верно).

Максимальное заглубление H₂ нижнего водоспуска ограничено требованием получения максимального расхода Q₂. Максимальный расход будет в том случае, если напор H₂ не вызовет отрыва потока в трубе от ее стенок, т.е. не превратит трубу в «отверстие в тонкой стенке» с m₀ < m_т (см. табл.4.1).

С использованием формулы (4.12) и понятия о давлении насыщенных паров [1] имеем при t = 20 °C, j_т = m_т и e = 0,64 (табл.4.1):

;

.

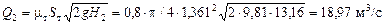Ответ: d_т = 1,361 м;

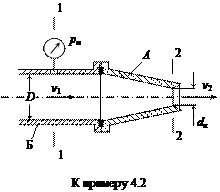
Пример 4.2. Определить расход воды через конический насадок А гидромонитора с выходным диаметром насадка d_н = 20 мм, если насадок присоединен к стволу Б гидромонитора через плавный переходник, а диаметр ствола D = 100 мм. Манометрическое давление перед насадком р_м = 100 ат.

Решение. Расход при истечении в атмосферу

Струя выходит из насадка, потеряв часть энергии в самом насадке (см. табл.4.1, z_н = 0,07). Кроме того, на скорость истечения v₂ влияет скорость подхода воды к насадку v₁. Поэтому составим уравнение Бернулли для сечений 1-1 и 2-2, проведя плоскость сравнения 0-0 по оси трубы:

где z₁ = z₂; предполагая режим движения в стволе Б турбулентным, примем 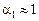; р₂ = 0, так как речь идет об избыточном давлении; в сжатом сечении струи a₂ = 1. После сокращений имеем:

.

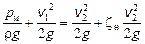Заменим, используя уравнение (3.5), скорость v₁ на v₂:

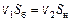или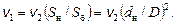

Тогда

.

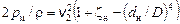Откуда

м/с.

Искомый расход

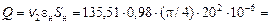
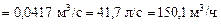
Ответ: Q = 150,1 м³/ч.

ЗАДАЧИ

Задача 4.1. Определить абсолютное давление в сечении С-С, уровень h воды в трубке над свободной поверхностью воды в чашке и расход Q при истечении из внешнего цилиндрического насадка диаметром d_н = 20 мм под постоянным напором Н = 2 м.

Ответ: р_абс = 83258 Па; h = 1,513 м; Q =1,613 л/с.

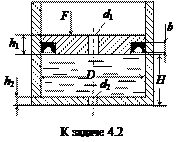
Задача 4.2. Определить суммарный расход Q масла АМГ-10 [1] из отверстия диаметром d₁ = 5 мм (в поршне) и диаметром d₂ = 5 мм (в днище цилиндра), если поршень массой m = 100 кг находится под нагрузкой F = 1000 Н.

Силу трения уплотняющей манжеты о стенки цилиндра определить по формуле

,

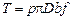где р – давление под поршнем; f – коэффициент трения резины по стали со смазкой (f = 0,01); b – ширина уплотняющей поверхности манжеты. Высоту слоя масла над поршнем не учитывать.

Дополнительно задано: высота слоя масла под поршнем H = 4 м; диаметр поршня D = 300 мм; ширина манжеты b = 10 мм; толщина поршня h₁ = 20 мм и днища h₂ = 10 мм.

Ответ: Q₁ + Q₂ = 16,61 л/мин.

Задача 4.3. Для условий задачи 4.2 определить соотношение расходов 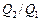через соответствующие отверстия в днище цилиндра и в поршне.

Задано: F = 10⁴H; m = 50 кг; Н = 5 м; D = 100 мм; d₁ = 8 мм; d₂ = 4 мм; h₁ = 16 мм; h₂ = 15 мм; b = 10 мм.

Ответ: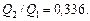

Задача 4.4. Цилиндр массой m = 100 кг надет подвижно на поршень диаметром D = 300 мм (условно – без протечек между поршнем и цилиндром и без трения).

В днище цилиндра выполнено отверстие диаметром d₁ = 5 мм, в поршне – отверстие диаметром d₂ = 4 мм. Толщина днища h₁ = 5 мм и поршня h₂ = 20 мм; H = 5 м. Определить соотношение скоростей истечения керосина (r = 806 кг/м³) из верхнего (v₁) и нижнего (v₂) отверстий и скорость v_ц опускания цилиндра.

Ответ: v₁/v₂ = 0,603; v_ц = 2,69 мм/с.

Задача 4.5. Определить скорость v_п движения поршня вниз под действием нагрузки F = 120 кН. Истечение масла И-25А [1, с.314] из-под поршня в атмосферу происходит через два одинаковых отверстия диаметром d = 10 мм. Поршень диаметром D = 200 мм уплотнен резиновой манжетой шириной b = 10 мм. Коэффициент трения манжеты о стальной корпус принять f = 0,15. Высота поршня а = 35 мм. Массой поршня пренебречь.

Ответ: v_п = 0,374 м/с.

Задача 4.6. Определить диаметр d₀ отверстия в тонкой стенке для заполнения емкости объемом V = 9,36 м³ за полчаса водой, если центр отверстия расположен ниже уровня воды в накопителе на отметке –2 м.

Ответ: d₀ = 41,3 мм.

Задача 4.7. Истечение из большого резервуара происходит через два одинаковых отверстия диаметром d = 60 мм, расстояние между центрами которых по вертикали h = 0,5 м.

Определить (с учетом совершенства сжатия струй) глубину H воды в резервуаре, при которой суммарный расход

Ответ: H = 2,632 м.

Задача 4.8. Малое квадратное отверстие со стороной а = 36 мм в тонкой вертикальной стенке примыкает одной стороной к дну.

Определить, при какой глубине Н воды в резервуаре расход через отверстие будет Q = 4,18 л/с.

Ответ: H = 1,467 м.

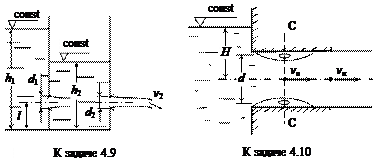
Задача 4.9. В вертикальной тонкой стенке, разделяющий резервуар на две части, выполнено отверстие диаметром d₁ = 50 мм. В боковой стенке правой части резервуара выполнено отверстие диаметром d₂. Оба отверстия расположены соосно и на уровне l = 1 м от дна. Истечение из среднего отверстия – под уровень, из правого – в атмосферу. Уровень воды в левой части h₁ = 2,5 м, в правой – h₂.

Определить уровень h₂ в правой части, диаметр d₂ и скорость истечения v₂ при расходе через среднее отверстие Q = 11,16 м³/ч.

Ответ: h₂ = 2,169 м; d₂ = 36,5 мм; v₂ = 4,646 м/с.

Задача 4.10. Через внешний цилиндрический насадок диаметром d = 38 мм истекает в атмосферу вода с расходом Q = 5,6×10^-3 м³/с. Определить напор H перед насадком, скорость v_н на выходе из насадка и скорость v_с в сжатом сечении, а также абсолютное давление р_абс в сечении С-С.

Ответ: H = 1,847 м; v_н = 4,937 м/с; v_с = 7,714 м/с; р_абс = 84394 Па.

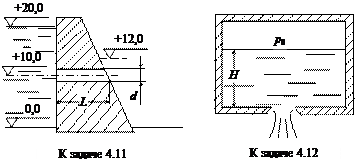
Задача 4.11. В теле железобетонной плотины выполнен водоспуск диаметром d и длиной L = 5 м, предназначенный для пропуска воды с расходом Q = 9 м³/с при свободном истечении. Водоспуск расположен на отметке Ñ = +10 м. Определить диаметр d. Определить также расход Q₂ при подъеме нижнего уровня воды до отметки Ñ = +12 м.

Ответ: d = 1,015 м; Q₂ = 8,069 м³/с.

Задача 4.12. Из резервуара с избыточным давлением р₀ = 0 истекает вода через донное отверстие с острыми кромками при высоте слоя воды Н = 3 м. Определить 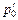для увеличения расхода вдвое и 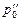для уменьшения расхода вдвое через то же отверстие.

Ответ:

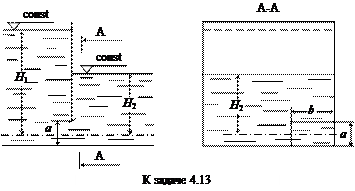
Задача 4.13. Определить расход воды через малое прямоугольное отверстие размерами а = 15 см, b = 20 см в тонкой вертикальной разделительной стенке при глубине погружения центра отверстия под свободной поверхностью с напорной стороны Н₁ = 4,4 м, с низконапорной Н₂ = 2 м. Отверстие расположено в нижнем углу разделительной стенки.

Ответ:

Задача 4.14.Определить расход воды Q из пожарной колонки А при манометрическом давлении в ней р_м = 3 кг/см², если отбор воды на пожаротушение осуществляется по горизонтали через гибкий рукав Б длиной l_р = 120 м диаметром d_р = 73 мм и конический сходящийся насадок В с выходным диаметром d_н = 20 мм. Диаметр колонки D_к = 100 мм; изгибами рукава пренебречь; коэффициент Дарси принять l = 0,025 для квадратичной зоны сопротивления.

Ответ: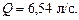

Задача 4.15. Для условий задачи 4.14 определить дальность полета компактной струи h_ком при любом угле a наклона насадка к горизонту, а также дальность полета раздробленной струи при a = 0, 30 и 60°. Скорость истечения воды из насадка принять v = 21,3 м/с.

Ответ: при a = 0° L = 28,36 м; при a = 30° L = 24,31 м; при a = 60° L = 21,68 м; h_ком = 16,82 м.

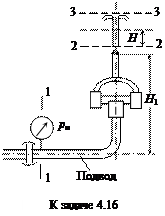
Задача 4.16. Для тушения пожара в условиях крутого падения пласта ствол гидромонитора установлен вертикально вверх; используется низконапорное оборудование. Расход воды Q = 30 л/с.

Длина компактной части струи Н = 29 м; длина трубы от точки установки манометра до входа в насадок l = 2,5 м; превышение насадка над осью подвода Н₁ = 1,2 м; насадок конический сходящийся с диаметром выходного отверстия d_н; условный проход труб гидромонитора D = 100 мм; суммарный коэффициент местных сопротивлений Sz = 30.

Высотой и сопротивлением насадка пренебречь. Сопротивлением воздуха пренебречь. Трубы стальные, сварные, с незначительной коррозией. Определить диаметр насадка d_н и потребное давление р_м.

Ответ: d_н = 36 мм; р_м = 6,9 ат.

Задача 4.17. Гидроцилиндр с двухсторонним штоком заполнен жидкостью без пустот при атмосферном давлении. В поршне выполнено одно сквозное отверстие по типу конического сужающего насадка (см. табл.4.1). К штоку попеременно прикладывают силу F (слева F₁, справа F₂); в результате перетока жидкости из одной полости цилиндра в другую по указанному отверстию в поршне последний перемещается вправо со скоростью v₁, затем влево – со скоростью v₂. Утечек по штоку и поршню нет.

Найти соотношение сил F₂/F₁, обеспечивающее одинаковую скорость движения поршня влево и вправо (v₂ = v₁ = v_п), если при движении поршня вправо:

1) отверстие в поршне работает как расширяющийся насадок (см. табл.4.1);

2) отверстие в поршне работает как отверстие в тонкой стенке с острой кромкой.

Ответ:1) F₂/F₁ = 3,92; 2) F₂/F₁ = 2,3.

Задача 4.18.Для условий задачи 4.17 найти соотношение скоростей v₂/v₁ при равенстве попеременно действующих сил F₁ = F₂ = F, если при движении поршня вправо:

1) отверстие в поршне работает как расширяющийся насадок;

2) отверстие в поршне работает как отверстие в тонкой стенке с острой кромкой.

Ответ: 1) v₂/v₁ = 1,98; 2) v₂/v₁ = 1,52.

Задача 4.19. Истечение в атмосферу происходит из отверстия с острой кромкой в крышке (заглушке) трубы диаметром D при манометрическом давлении р_м = 3 ат с расходом Q = 30,6 л/с. Определить диаметр трубы D, если диаметр отверстия d₀ = 50 мм.

Ответ: D » 100 мм.

Задача 4.20. В боковой вертикальной стенке резервуара выполнено прямоугольное отверстие шириной b = 0,5 м и высотой а. Расстояние верхней кромки отверстия до свободной поверхности воды Н₁ = 2 м. Определить высоту а отверстия из условия пропуска через него воды с расходом Q = 1 м³/с.

Коэффициент расхода m принять согласно пояснениям к формуле (4.13).

Ответ: а = 0,498 м.

Задача 4.21. Определить коэффициент расхода струеформирующего устройства (СФУ) и его вид (см. табл.4.1) при истечении воды через это СФУ в дне вертикального цилиндрического открытого бака диаметром D = 1,4 м, если диаметр СФУ d = 20 мм, а уровень воды в баке понизился за t = 38 мин от уровня Н₁ = 2,6 м до уровня Н₂ = 1,2 м.

Ответ: m = 0,5.

Задача 4.22. Из полностью заполненной горизонтальной цистерны диаметром D = 2,21 м и длиной L = 8,2 м сливают жидкость через сложное СФУ с коэффициентом расхода m = 0,62. Определить время полного опорожнения цистерны при диаметре СФУ d = 100 мм.

Ответ: t = 27,8 мин.

Задача 4.23. Для условий задачи 4.22 найти соотношение времени опорожнения верхней и нижней частей цистерны.

Ответ: t₁/t₂ = 0,547.

Задача 4.24. Вертикальный цилиндрический резервуар с водой диаметром D = 4 м и высотой Н = 60 м имеет в дне центральное отверстие с острой кромкой. Определить время t полного опорожнения резервуара при диаметре отверстия d₀ = 0,1 м.

Ответ: t = 47,6 мин.

Задача 4.25. Вода истекает в атмосферу через боковое отверстие диаметром d = 2,5 см (с острой кромкой) в стенке вертикального цилиндрического резервуара диаметром D = 8 м. Определить время t снижения уровня воды от отметки Ñ₁ = +12 м до отметки Ñ₂ = + 4,5 м. Нулевая отметка проходит через ось отверстия.

Ответ: t = 27,82 ч.

Задача 4.26. В вертикальном цилиндрическом резервуаре диаметром D = 6 м находится слой воды высотой Н_в = 1,1 м и слой нефти (r_н = 900 кг/м³) высотой Н_н = 6,2 м. Определить время t слива воды через донный цилиндрический наружный насадок диаметром d_н = 0,1 м.

Ответ: t = 7,35 мин.

Задача 4.27. Из одного резервуара в другой перепускают жидкий нефтепродукт (n = 25×10^-6 м²/с) через короткую трубу с l/d = 5 при диаметре трубы d = 100 мм и шероховатости D = 0,1 мм. Диаметры резервуаров одинаковы и равны D = 8 м. Уровни жидкости в начале процесса Ñ₁ = +8 м, Ñ₂ = +0,4 м. Нулевая плоскость проходит через ось трубы. Приняв коэффициент расхода при истечении через трубу в среднем m = 0,7, определить время t выравнивания уровней до их разности 0,02 м.

Ответ: t = 1,5 ч.

Задача 4.28. Из цилиндрического вертикального бака с площадью поперечного сечения S_б = 0,95 м² вытекает вода через донное СФУ с площадью проходного отверстия S₀ = 3 см². Через t = 30 мин после открытия СФУ высота слоя воды в баке оказалось равной Н₂ = 25 см. Сколько литров воды вытекло за первые 10 мин? Коэффициент расхода СФУ принять равным m₀ = 0,62.

Ответ: V = 569 л.

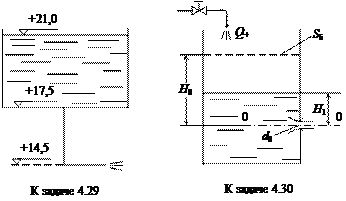
Задача 4.29. Определить время t опорожнения цилиндрического бака площадью S_б = 4 м², если начальная отметка уровня воды в нем Ñ₁ = +21 м; отметка дна бака Ñ₂ = +17,5 м; отметка выхода сливной трубы в атмосферу Ñ₃ = +14,5 м. Диаметр трубы d = 0,2 м, ее шероховатость D_э = 0,1 мм; труба имеет прямое колено с a = 90°.

Ответ: t = 3,15 мин.

Задача 4.30. Вода истекает из цилиндрического бака площадью S_б = 1,2 м² через малое боковое отверстие в тонкой стенке диаметром d = 30 мм. В резервуар вода поступает с постоянным расходом Q₊ = 2,5×10^-3 м³/с. Определить уровень воды Н₀ по отношению к оси отверстия 0-0 через t = 20 мин после открытия этого отверстия (запорный орган не показан), если в момент открытия напор перед отверстием составлял Н₁ = 1,2 м.

Использовать способ последовательных приближений.

Ответ: Н₀ = 1,455 м.

Задача 4.31. Насос подает эмульсию в верхний бак с расходом Q₊ = 6 л/с. Высота бака до сливной трубки Н₀ = 1,4 м, диаметр D = 1,6 м. Эмульсия отводится к потребителю через донное составное СФУ с диаметром проходного отверстия d = 25 мм и коэффициентом расхода m = 0,55. Определить продолжительность t работы насоса для наполнения бака до отметки сливной трубки, если при его пуске высота слоя эмульсии в баке составила Н₁ = 0,1 м при открытом СФУ.

Ответ: t = 8 мин 49 с.

Задача 4.32. Жидкость из цилиндрического вертикального резервуара А диаметром D = 1,8 м, наполненного до уровня Н = 2,2 м, перетекает в цистерну Б через донное СФУ (d_с = 40 мм, m_с = 0,82) и заливочную воронку В, имеющую суммарный коэффициент сопротивления z_в = 0,7, отнесенный к скорости жидкости v_в в цилиндрической части воронки с d_в = 50 мм, и высоту h_в = 0,5 м. Определить высоту Н₁ слоя жидкости в резервуаре А, при которой жидкость безусловно сливается в цистерну через воронку, и соответствующий объем V₁.

Пропускная способность СФУ и воронки различна. Если пропускная способность воронки меньше, чем у СФУ, часть жидкости через ловитель Г отводится в бачок Д, откуда позже насосом возвращается в резервуар А.

Ответ: H₁ = 1,0675 м; V₁ = 2,715 м³.

Задача 4.33. Для условий задачи 4.32 определить объем V₂ из слоя DН = Н – Н₁, слившийся в цистерну через воронку В, и вместимость V₃ сливного бачка Д.

Ответ: V₂ = 2,365 м³; V₃ ³ 515,5 л.

Задача 4.34. Определить давление воды р в статическом режиме (р = const) при допускаемом напряжении материала трубы (сталь) на растяжение [s]_p = 112,8 МПа и напряжение в материале трубы s_уд при мгновенной остановке воды, двигавшейся со скоростью v₀ = 2 м/с при температуре t = 20 °C, если давление перед задвижкой до ее закрытия составляло р₀ = 1,5 МПа, а также определить запас прочности трубы n = [s]_p/s_уд. Диаметр трубы D = 205 мм, толщина стенки трубы d = 10,5 мм.

Ответ: р = 11,56 МПа; s_уд » 40 МПа; n = 2,82.

Задача 4.35. Стальной пульповод протяженностью L = 15 км служит для гидротранспортирования угольной пульпы от шахты (пункт А) до обогатительной фабрики (пункт В). В данный момент пульпопровод заполнен промывочной водой с избыточным давлением р = 0,49 МПа при температуре Т = 10 °С и герметично закрыт с обоих концов.

При выполнении ремонтных работ пульпопровод получил пробоину (разгерметизировался). Аппаратура на станциях А и В отметила изменение давления с интервалом 10 с. Установить место разгерметизации рабочей нитки пульповода, если его диаметр d = 300 мм, а толщина стенки d = 10 мм.

Ответ:место разрыва от станции А на расстоянии 1,38 км.

Задача 4.36. Определить давление воды в стальной трубе после мгновенного закрытия задвижки, если до ее закрытия существовало избыточное давление р₀ = 5 кг/см², а скорость воды v₀ = 1 м/с. Диаметр трубы d = 0,5 м, толщина стенок d = 5 мм. Температура воды Т = 20 °С.

Ответ: р = 1,64 МПа.

Задача 4.37. По стальному трубопроводу длиной l = 500 м и диаметром d = 150 мм осуществляют шахтный водоотлив насосом с расходом Q = 250 м³/ч при температуре воды Т = 20 °С. Насос расположен на отметке Ñ₁ = –50 м, зумпф – на отметке Ñ₂ = +50 м. Трубопровод оснащен двумя задвижками: после насоса (нижняя) и перед зумпфом (верхняя). Рабочий напор насоса Н_{н, раб} = 300 м вод.ст. Определить минимально допустимое время t_min закрытия верхней задвижки из расчета максимально возможного повышения давления перед ней в 1,5 раза. Шероховатость труб принять D_э = 0,17 мм. Местные сопротивления учесть по правилу «длинного» трубопровода.

Ответ: t_min = 1,88 c.

Задача 4.38. В трубопроводе диаметром d = 100 мм и длиной l = 1 км в результате закрытия дальней задвижки за t_з = 1,6 с давление воды перед ней повысилось на величину Dр = 0,6 МПа. Определить скорость v₀ движения воды в трубопроводе до закрытия задвижки, если трубы: а) чугунные, d = 5 мм; б) стальные, d = 6 мм.

Температура воды Т = 10 °С, начальное давление перед задвижкой р₀ = 5 МПа.

Ответ: а) v₀ = 0,480 м/с; б) v₀ = 0,486 м/с.