
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
РАЗДЕЛ 3
УРАВНЕНИЕ БЕРНУЛЛИ
Количество жидкости, проходящее через живое сечение (ЖС) в единицу времени, называют расходом. Различают расходы:
· объемный
 м3/с; (3.1)
м3/с; (3.1)
· массовый
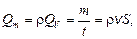 кг/с; (3.2)
кг/с; (3.2)
· весовой
 Н/с. (3.3)
Н/с. (3.3)
На пути движения жидкости (рис.3.1) конфигурация потока и поле скоростей в его живом сечении (ЖС) могут изменяться, но количество жидкости, прошедшее за время t через любое сечение, неизменно, это фиксируется уравнением неразрывности:
 (3.4)
(3.4)
Для капельной жидкости ее плотность r мало зависит от величины давления р (по крайней мере, при изменении р в пределах 10 МПа). При r = const выражение (3.4) будет соответствовать закону постоянства объемного расхода на рассматриваемом участке потока:
 . (3.5)
. (3.5)

|
Для газа плотность r зависит от давления р и температуры T, поэтому при расчете газопроводов используют зависимости (3.4) и (3.2), при этом
 , (3.6)
, (3.6)
где R – газовая постоянная, для воздуха 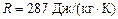 ; Т – абсолютная температура, К; р – давление.
; Т – абсолютная температура, К; р – давление.
Полный запас энергии Е некоторого объема жидкости массой m относительно произвольной горизонтальной плоскости сравнения определяется выражением
 (3.7)
(3.7)
где mgz = Ez – потенциальная энергия положения, Дж; z – вертикальная координата точки или тела (z положительна, если тело расположено выше плоскости сравнения, и отрицательна – если ниже);  – потенциальная энергия давления, Дж;
– потенциальная энергия давления, Дж;  – кинетическая энергия, Дж.
– кинетическая энергия, Дж.
Энергия, отнесенная к массе m, объему V или весу G, называется удельной энергией. Так, энергия, приходящаяся на единицу массы,
 Дж/кг. (3.8)
Дж/кг. (3.8)
Энергию, приходящуюся на единицу объема (т.е. давление), получим, разделив выражение (3.7) на V; при этом  ,
,
 Дж/м3 = Па. (3.9)
Дж/м3 = Па. (3.9)
Энергию, приходящуюся на единицу веса (т.е. напор), получим, разделив (3.7) на G; при этом G = mg,
 Дж/Н = м. (3.10)
Дж/Н = м. (3.10)
Связь между давлением р и напором Н выражается согласно выражению (2.3) формулой
р = rgH. (3.11)
При движении реальной жидкости (r = const, m > 0) кинетическая энергия в сечении потока может распределяться по-разному в зависимости от режима движения и вида потока. Так, при ламинарном режиме эпюра скоростей в ЖС – парабола, при равномерном установившемся турбулентном движении эта эпюра напоминает трапецию, для струи – прямоугольник, т.е. степень равномерности распределения кинетической энергии в ЖС потока для разных условий различна. Это отражается через коэффициент Кориолиса, который вводят в состав кинетической энергии в формулах (3.8)-(3.10) как множитель a. Для Re < 2320 a = 2; для Re > 2320 при равномерном движении турбулентного потока a = 1,03-1,10. С целью упрощения расчетов в последнем случае рекомендуется принимать a » 1. Для струи и идеальной жидкости a = 1.
В сечении 1-1 полная энергия (рис.3.1)
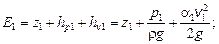
в сечении 2-2

потерянная между сечениями 1-1 и 2-2 часть энергии составит

Здесь закон сохранения энергии имеет вид

или
 . (3.12)
. (3.12)
Уравнение (3.12) есть уравнение Бернулли для реального потока капельной жидкости.
Потери энергии (напора) по длине потока определяются формулой Дарси
 (3.13)
(3.13)
где l – коэффициент гидравлического трения (или коэффициент Дарси).
Участок потока, где скорость изменяет свое направление и значение, называют местным сопротивлением (МС). Протяженность МС мала по сравнению с длиной прямых участков, поэтому считают, что МС длины не имеет. Эти потери определяются по формуле Вейсбаха:
 (3.14)
(3.14)
где z – коэффициент местного сопротивления.
Коэффициент Дарси в общем случае зависит от режима движения (Re) и шероховатости (D) твердых границ потока, т.е.
 . (3.15)
. (3.15)
Число Рейнольдса Re (безразмерное) характиризует соотношение сил инерции (через среднюю скорость v) и сил вязкого трения (через кинематический коэффициент вязкости n)
 (3.16)
(3.16)
где  ; L – характерный размер ЖС.
; L – характерный размер ЖС.
Для ЖС круглой формы диаметром d L = d; для ЖС некруглой формы L = 4Rг; Rг – гидравлический радиус,
 (3.17)
(3.17)
где SЖС – площадь живого сечения, м2; c – смоченный периметр, м.
Смоченный периметр – это длина линии контакта жидкости с твердыми стенками в ЖС (длина свободной поверхности жидкости в смоченный периметр не входит).
Для ламинарного режима движения (линейная зона сопротивления,  )
)
0 < Re < 2320 и  . (3.18)
. (3.18)
Для общего случая турбулентного режима (Re > 2320) по А.Д.Альтшулю
 (3.19)
(3.19)
где Δэ – эквивалентная (зернистая) шероховатость, мм.
Турбулентный режим подразделяют на три зоны сопротивления, границы между которыми ориентировочно соответствуют:
· зоне гладкого трения или зоне гидравлически гладких труб, когда толщина δ ламинарного пристенного слоя больше высоты Δ (или Δэ) шероховатостей, т.е. δ > Δ. При этом lII ≠ f(Δ). Эта зона соответствует  , а коэффициент l может быть определен по Блазиусу
, а коэффициент l может быть определен по Блазиусу
 ; (3.20)
; (3.20)
· зоне гидравлически шероховатых труб, когда δ ≤ Δ. При этом ядро потока дополнительно турбулизируется, касаясь выступов шероховатости, и lIII = f (Re, Δ). Эта зона примерно соответствует
 (3.19)
(3.19)
· квадратичной зоне сопротивления (  ), когда δ → 0, а
), когда δ → 0, а  и не зависит от скорости потока v. Эта зона соответствует
и не зависит от скорости потока v. Эта зона соответствует  и по Шифринсону
и по Шифринсону
 (3.21)
(3.21)
В справочниках приводятся значения l для квадратичной зоны сопротивления. В табл.3.1 даны значения эквивалентной шероховатости для некоторых видов труб [1, 5].
Таблица 3.1
| Вид и состояние труб | Δэ, мм |
| Трубы тянутые из стекла и цветных металлов, новые | 0,001-0,002 |
| Трубы тянутые стальные бесшовные, новые | 0,01-0,02 |
| То же, после нескольких лет эксплуатации | 0,15-0,30 |
| То же, после длительной эксплуатации, со следами коррозии | 0,50-2,0 |
| Трубы стальные сварные, новые | 0,03-0,10 |
| То же, с незначительной коррозией | 0,10-0,20 |
| То же, сильно заржавленные | 0,80-1,50 |
| Трубы чугунные, новые | 0,20-0,50 |
| То же, бывшие в эксплуатации | 0,50-1,50 |
| Трубы бетонные | ~0,5 |
Коэффициенты местных сопротивлений z в общем случае зависят от режима движения (Re), расстояния между двумя МС (L), степени открытия запорного устройства и от вида МС.
В квадратичной зоне сопротивления  . Справочники приводят сведения о z именно для этой зоны.
. Справочники приводят сведения о z именно для этой зоны.
При ламинарном движении нужно учитывать поправку В к формуле (3.14), которая для потерь давления будет иметь вид:
 (3.22)
(3.22)
где указанная поправка может быть ориентировочно определена из следующих данных [10]:
| Re | ³2300 | |||||||||
| B | 2,5 | 1,7 | 1,6 | 1,4 | 1,3 |
Все справочные данные приводятся для одиночного МС, к которому жидкость подходит с неискаженной эпюрой скоростей u.
К таким эпюрам относится парабола (ламинарный режим; a = 2,  ), описываемая формулой
), описываемая формулой
 , (3.23)
, (3.23)
где J – гидравлический уклон,
 ; (3.24)
; (3.24)
Dhl и Dpl – потери соответственно напора и давления по длине потока l; ν – кинематический коэффициент вязкости, м2/с; r – радиус трубы, м; y – текущая координата для рассматриваемого слоя жидкости.
Любое МС искажает поле скоростей. Если между двумя смежными МС расстояние L недостаточно для восстановления нарушенной эпюры, то к МС № 2 поток подойдет с искаженной эпюрой, и коэффициент z2 не будет соответствовать указанному в справочнике или полученному расчетом. По опытным данным общий коэффициент нескольких близко расположенных МС бывает меньше арифметической суммы отдельных z, присущих этим МС, т.е.  [9].
[9].
Базовой длиной между двумя МС, достаточной для выравнивания поля скоростей, считают
 (3.25)
(3.25)
Расчетным путем можно определить потери энергии:
· от внезапного расширения потока от сечения S1 до сечения S2 > S1
 (3.26)
(3.26)
при S2 >> S1 (выход потока из трубы в резервуар с v » 0)  ;
;
· от внезапного сужения потока от сечения S1 до сечения S2 < S1
 (3.27)
(3.27)
при S1 >> S2 (вход в трубу из резервуара)  .
.

|
Данные о z при сочленении двух плавных колен приведены на рис.3.2 [1].
Коэффициент сопротивления диафрагмы ζд, расположенной внутри трубы постоянного сечения (рис.3.3),
 (3.28)
(3.28)
где  ; εд – коэффициент сжатия струи (по А.Д.Альтшулю [5]),
; εд – коэффициент сжатия струи (по А.Д.Альтшулю [5]),
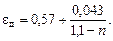 (3.29)
(3.29)

|
Коэффициент сопротивления сварного стыка на трубопроводе
 (3.30)
(3.30)
где δ – высота сварного стыка (шва), выступающего внутрь трубы; d – внутренний диаметр трубы.
Возрастание гидравлического сопротивления, вызванное сварными швами, определяется формулой
 (3.37)
(3.37)
где l1, l – сопротивление трубопровода, соответственно, с учетом и без учета сварных швов; l – расстояние между стыками (длина труб).
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 3.1.Определить направление движения реальной жидкости и вид местного сопротивления в наклонном трубопроводе при следующих исходных данных:
геодезическая отметка сечений z1 = 2 м, z2 = 6 м;
манометрическое давление p1 = 0,1 МПа, p2 = 0,05 МПа;
диаметры трубопровода d1 = 200 мм, d2 = 120 мм;
расход жидкости 
кинематический коэффициент вязкости жидкости 
Решение. Жидкость должна двигаться от области с большей полной удельной энергией в область с меньшей энергией.
Полная удельная энергия в сечении 1-1 и 2-2 согласно (3.12):
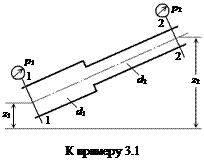
|


Жидкость движется от сечения 1-1 к сечению 2-2, если Е1 > Е2, и наоборот.
Для определения Е1 и Е2 нужны сведения о средних скоростях v1 и v2, коэффициентах Кориолиса a1 и a2 и плотности r. Используя формулу расхода (3.5), имеем




Коэффициент Кориолиса зависит от режима движения и вида потока. В задаче поток напорный, т.е. для круглого сечения
 – ламинарный режим; a = 2;
– ламинарный режим; a = 2;
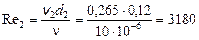 – турбулентный режим; a » 1.
– турбулентный режим; a » 1.
Заданному ν согласно табл.1.1 соответствует жидкость из группы минеральных масел  . Для более точного установления r можно воспользоваться справочными данными, например [1, с.314], жидкости с
. Для более точного установления r можно воспользоваться справочными данными, например [1, с.314], жидкости с  соответствует масло АМГ-10,
соответствует масло АМГ-10, 
При этом:

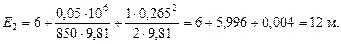
Так как Е1 > Е2, масло движется от сечения 1-1 к сечению 2-2, а местное сопротивление называется внезапным сужением потока.
Пример 3.2. Вода для поливки улиц поступает из накопителя в цистерну емкостью V = 10 м3 за время t по трубопроводу диаметром (условный проход) d = 50 мм и длиной l = 10 м. На трубопроводе имеется регулируемый пробковый кран с коэффициентом местного сопротивления zкр. При zкр = 40 цистерна наполняется за t1 = 1 ч. На какой угол β надо установить рукоятку крана, чтобы вдвое сократить время наполнения цистерны (t2 = 0,5 ч)? Принять для трубопровода трубу стальную тянутую, новую; высотой h пренебречь. Уровень воды в накопителе за время заправки цистерны постоянен. Данные для решения:

|
| b, град | |||||||
| zкр | 0,4 | 1,9 |
Решение. Составим уравнение Бернулли по типу (3.12), включающее данные о потерях в местных сопротивлениях. С этой целью проведем плоскость сравнения 0-0 по оси трубы, зададим начальное сечение 1-1 по свободной поверхности воды в накопителе, а сечение 2-2 на выходе из трубы. Тогда:

где z1 = H; z2 = 0; р1 = р2 = ра; v1 » 0;  ;
;  – вход из накопителя в трубу;
– вход из накопителя в трубу;  – для прямого колена с a = 90° [1].
– для прямого колена с a = 90° [1].
После подстановки названных величин имеем:

Для решения этого уравнения необходимо иметь сведения о средней скорости v2, коэффициенте Кориолиса a2 и коэффициенте Дарси l. Обозначим v2 через v.
Согласно (3.1)

Определим режим движения, приняв для воды  (см. табл.1.5),
(см. табл.1.5),

т.е. режим турбулентный и a » 1.
Уточним зону сопротивления. Для указанных в задании труб шероховатость Δэ = 0,015 мм (табл.3.1). Тогда 
 и
и  т.е. Re = 70750 относится к третьей зоне сопротивления, где l определяется формулой Альтшуля
т.е. Re = 70750 относится к третьей зоне сопротивления, где l определяется формулой Альтшуля

Находим напор в накопителе:


Выразим новое значение

где vнов – новая средняя скорость в трубе, 

При этом  aнов » 1.
aнов » 1.
Полученное Re также относится к третьей области сопротивления:
 ,
,
т.е. 

Согласно данным для решения в условии примера на приведенном рисунке zкр = 4,45 соответствует примерно углу установки крана β » 26о. Так как начальная величина zкр = 40 соответствовала b » 45о, кран следует приоткрыть. Заметим, что изменение угла b примерно в 1,7 раза вызвало изменение сопротивления крана примерно в 9 раз и сократило время заправки цистерны в 2 раза.
ЗАДАЧИ
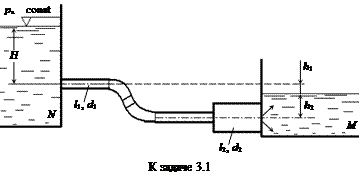
Задача 3.1.Жидкость перетекает при H = const из резервуара N в резервуар M по трубопроводу, состоящему из двух участков (  ,
,  ) разного диаметра (d1 = 50 мм, d2 = 100 мм), при одинаковом коэффициенте Дарси (l1 = l2 = 0,03). На трубопроводе имеются два плавных колена (zк = 0,15) и внезапное расширение (zвр).
) разного диаметра (d1 = 50 мм, d2 = 100 мм), при одинаковом коэффициенте Дарси (l1 = l2 = 0,03). На трубопроводе имеются два плавных колена (zк = 0,15) и внезапное расширение (zвр).
Определить расход жидкости Q при Н = 1 м и h1 = 0,25 м.
Ответ: Q = 2,2 л/с.
|
Задача 3.2.Жидкость перетекает из бака N в бак М по трубопроводу, состоящему из двух прямых отрезков (  ,
,  ) разного диаметра (d1 = 0,1 м, d2 = 0,15 м) при одинаковом коэффициенте Дарси (l1 = l2 = 0,03). Высоты слоя жидкости в баках: Н1 = 4 м, Н2 = 2 м.
) разного диаметра (d1 = 0,1 м, d2 = 0,15 м) при одинаковом коэффициенте Дарси (l1 = l2 = 0,03). Высоты слоя жидкости в баках: Н1 = 4 м, Н2 = 2 м.
1. Определить расход жидкости Q.
2. Построить напорную линию (НЛ) и пьезометрическую (ПЛ) от бака N до бака М.
Ответ: Q = 18 л/с.
Задача 3.3.Из реки в колодец с расходом Q = 10 л/c поступает вода через приемный фильтр (zф = 12) и трубопровод (  ; d = 0,1 м); коэффициент Дарси принять l = 0,022.
; d = 0,1 м); коэффициент Дарси принять l = 0,022.
По достижении разности уровней воды в реке и колодце Н автоматически включается насос, подающий воду с тем же расходом на производственные нужды.
Определить величину Н.

|
Ответ: Н = 3,34 м.

|
Задача 3.4.Из большого резервуара вода подводится к пункту потребления под напором Н по горизонтальному трубопроводу общей длиной  и одинаковым диаметром d = 0,15 м. Трубопровод смещен в середине пролета в горизонтальной плоскости с помощью двух плавных колен (zк = 0,44), установленных близко друг к другу.
и одинаковым диаметром d = 0,15 м. Трубопровод смещен в середине пролета в горизонтальной плоскости с помощью двух плавных колен (zк = 0,44), установленных близко друг к другу.
Определить напор Н, если пропускная способность трубопровода Q = 0,05 м3/с; принять коэффициент Дарси l = 0,025. Построить для трубопровода напорную линию (НЛ) и пьезометрическую (ПЛ).
Ответ: Н = 6,8 м.
Задача 3.5.В нижнем баке существует манометрическое давление рм над свободной поверхностью воды. Под действием этого давления вода с расходом Q транспортируется по вертикальному трубопроводу в верхний открытый бак.
Дано: d = 0,025 м,  , Q = 1,5 л/с. Принять коэффициент Дарси l = 0,035, режим – турбулентный, zз = 9,3.
, Q = 1,5 л/с. Принять коэффициент Дарси l = 0,035, режим – турбулентный, zз = 9,3.
Определить рм.
Ответ: 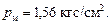
Задача 3.6.Центробежный насос (ЦН) забирает воду из колодца по всасывающей трубе (ВТ) длиной L1 = 12 м через приемный клапан с сеткой (zф1 = 6).

|
Колодец сообщается с большим водоемом самотечной трубой (СТ) с сеткой (zф2 = 2); длина СТ L2 = 20 м.
Расход ЦН и пропускная способность СТ одинаковы.
Определить расход Q и разность уровней воды в водоеме и колодце Z, если d1 = d2 = d = 150 мм, допустимая вакуумметрическая высота ЦН [Нвак] = 6 м, коэффициент Дарси для ВТ и СТ одинаков (l = 0,03), а ось ЦН расположена выше уровня воды в водоеме (h = 2 м).
Ответ: Q = 38 л/с; Z = 1,9 м.
Задача 3.7.Определить расход воды Q, истекающей из конического насадка в атмосферу, если в герметичном резервуаре большой емкости уровень воды постоянен и составляет Н = 5 м, а на свободной поверхности в резервуаре имеет место избыточное давление р = 0,4 МПа.
Размеры трубопровода:  ;
;  ; d1 = 100 мм; d2 = 200 мм; dн = 80 мм.
; d1 = 100 мм; d2 = 200 мм; dн = 80 мм.
Принять коэффициенты Дарси l1 = 0,043; l2 = 0,034 и коэффициенты местных сопротивлений: вентиля zв = 4, насадка zн = 0,06. Сжатием струи на выходе из насадка пренебречь; учесть другие  указанные на схеме местные сопротивления. Построить пьезометрическую линию для трубопровода в целом.
указанные на схеме местные сопротивления. Построить пьезометрическую линию для трубопровода в целом.

|
Ответ: Q = 68,2 л/с.
Задача 3.8.Вода вытекает в атмосферу по горизонтальной трубе, на которой установлены два пьезометра.
Диаметр трубы d = 50 мм, длина каждого из трех участков l = 4 м, разность показаний пьезометров Δh = 0,3 м.
Определить расход Q и напор в резервуаре Н.
Принять шероховатость трубы Δэ = 0,5 мм и кинематическую вязкость воды ν = 1 Ст; местными сопротивлениями пренебречь.
Ответ: Q = 2,85 л/с, Н = 0,9 м.

|
Задача 3.9.Определить режим безнапорного движения воды (число Рейнольдса) в прямоугольном лотке шириной b = 80 см при высоте слоя воды в нем h = 38 см, если расход составляет Q = 5,5 м3/ч, а температура воды t = 10°С.
Ответ:Re = 3004.
Задача 3.10.Определить расход воды Q, протекающей из бака А в бак В, и располагаемый напор Н, если показание ртутного дифманометра, присоединенного одним коленом к баку А, а другим – к середине трубы, составляет h = 440 мм.

|
Длина трубы l = 10 м, диаметр трубы d = 25 мм, ее шероховатость Δэ = 0,2 мм. Местные сопротивления учесть.
Ответ: Q = 1,8 л/с, Н » 10,1 м.
Задача 3.11.Из накопителя А с постоянным уровнем периодически и кратковременно выпускают часть воды по самотечному трубопроводу с расходом Q = 126 м3/ч.
Трубопровод стальной, эксплуатируется несколько лет и имеет следующие размеры:
· верхний горизонтальный участок с шиберной задвижкой (ЗШ) – l1 = 10 м, d1 = 100 мм;
· вертикальный участок – l2 = 5 м, d2 = d1;
· нижний горизонтальный участок – l3 = 30 м, d3 = 150 мм.
Выпуск воды производят при полностью открытой ЗШ. Резерв высоты h в накопителе для твердого осадка равен 0,27 м; участки соединены между собой прямыми коленами с a = 90°.
Определить высоту Н слоя воды в накопителе во время выпуска. Определение зоны сопротивления обязательно.
Ответ: Н » 2 м.

|
Задача 3.12.Вода при температуре t = 10° С вытекает по горизонтальному трубопроводу в атмосферу при постоянном напоре Н = 1,8 м.
Определить расход воды Q, если:
· внутренний диаметр трубы d = 6,2 см;
· задвижка шиберная (ЗШ) полностью открыта;
· труба стальная, бывшая в употреблении;
· длина трубопровода l = 10 м.
Ответ: Q = 7,24×10-3 м3/с.
Задача 3.13.По наклонной прямой трубе длиной L = 2 км постоянного диаметра d = 100 мм перекачивают нефть (ρ = 950 кг/м3, n = 25×10-6 м2/с) с расходом Q = 5 л/с. Избыточное давление в начале трубы р1 = 0,3 МПа.
Определить угол a наклона трубы к горизонту, если в конце трубы давление атмосферное. Изобразить трубу по итогам расчета.
Ответ:a = 24¢.
Задача 3.14.По трубе внутренним диаметром d = 100 мм перекачивают нефть плотностью  со средней скоростью v = 1,1 м/с.
со средней скоростью v = 1,1 м/с.
Определить суточную пропускную способность трубы (массовый расход Qт).
Ответ: Qт = 641,6 т/сут.
Задача 3.15.Определить часовой расход Q воды при ее движении безнапорно по желобу прямоугольной формы (ширина желоба а = 40 см, высота слоя воды h = 18 см) с числом Рейнольдса Re = 20000.
Ответ: Q = 13,7 м3/ч.

|
Задача 3.16.Горизонтальная труба диаметром d1 = 20 см в сечении а-а резко переходит в трубу диаметром d2 = 10 см.
Пренебрегая сопротивлениями и считая режим движения жидкости турбулентным, определить разность Δh1 уровней жидкости в пьезометрах, если в широком сечении жидкость движется со средней скоростью v = 0,8 м/с.
Как изменится Δh, если учесть местное сопротивление (резкое сужение)?
Ответ:Δh1 » 0,49 м; Δh2 = 0,685 м.

|
Задача 3.17.Определить манометрическое давление в сечении 1-1 (р1) трубопровода, по которому движется жидкость плотностью r = 880 кг/м3, если средняя скорость в сечении 1-1 v1 = 1,1 м/с и площадь живого сечения 2-2 (S2) в 2,5 раза меньше S1.
Расчеты выполнить для двух случаев, показанных на рисунке. Принять манометрическое давление в сечении 2-2 р2 = 2×105 Па, разность геодезических отметок сечений ΔZ = 8,7 м, жидкость считать идеальной.
Ответ: р1 = 2,78×105 Па (рисунок, а); р1 = 1,28×105 Па (рисунок, б).
Задача 3.18.Определить среднюю скорость движения воды в сечении 2-2 v2, если v1 = 1,2 м/с, манометрическое давление р1 = 1,2 кгс/см2 и р2 = 1,1 кгс/см2, а разность геодезических отметок сечений 1-1 и 2-2 составляет ΔZ = 3 м.
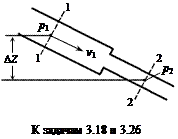
|
Принять режим движения турбулентным, потери напора на преодоление всех гидравлических сопротивлений между сечениями 1-1 и 2-2 ΣΔh1-2 = 1,4 м.
Ответ: v2 = 7,25 м/с.
Задача 3.19.Пожарный рукав диаметром d1 = 76 мм заканчивается коническим сходящимся насадком (брандспойтом), суммарные потери напора в котором составляют Δh = 0,3 м при расходе Q = 8×10-3 м3/с.

|
Определить манометрическое давление р1 на входе в насадок, если струя воды поднялась на высоту Н = 26 м. Сопротивлением воздуха пренебречь.
Ответ: р1 = 2,57×105 Па.
Задача 3.20.На какую высоту h может подняться вода из открытого резервуара А по трубке, присоединенной к узкому сечению S2 трубопровода, если средняя скорость воды в широком сечении v1 = 1,2 м/с, а манометрическое давление р1 = 12000 Па?
При этом площадь широкого сечения S1 в пять раз больше S2. Потерями энергии пренебречь.
Ответ: h = 0,538 м.
Задача 3.21.По трубопроводу, имеющему сужение, движется вода с расходом Q = 22 л/с. Диаметр трубопровода в широком сечении d1 = 200 мм, манометрическое давление там же р1 = 12000 Па.
Каким должен быть диаметр d2 узкой части трубопровода, чтобы обеспечить подъем воды из открытого резервуара А на высоту h = 3,1 м? Потерями напора пренебречь.
Ответ d2 » 55,1 мм.

|
Задача 3.22.По трубопроводу постоянного сечения длиной L = 56,4 км перекачивают нефть плотностью r = 860 кг/м3. Начальная отметка трубопровода выше конечной на 120 м.
Определить величину гидравлического уклона I, если манометрическое давление в начале трубопровода р1 = 3×106 Па, а в конце – атмосферное р2 = ра.
Ответ: I = 0,0084.

|
Задача 3.23.Определить манометрическое давление р2 в точке 2 водопровода постоянного диаметра, имеющего общую длину L1-2 = 12 км и L2-3 = 4,2 км, если в точке 3 давление р3 = ра, а в точке 1 манометрическое давление р1 = 1,5 МПа. Геодезические отметки точек: z1 = 0, z2 = 64 м, z3 = 42 м.
Ответ: р2 = 0,165 МПа.
Задача 3.24.Водомер Вентури имеет диаметры d1 = 200 мм, d2 = 100 мм. Определить расход воды Q, если показание ртутного дифманометра соответствует Δh = 4,2 см. Принять коэффициент Кориолиса a = 1,06 и коэффициент расхода, учитывающий потери энергии в водомере m = 0,96.
Ответ: Q » 24,4×10-3 м3/с.
Задача 3.25.На горизонтальном участке трубопровода внутренним диаметром d1 = 100 мм установлен водомер Вентури с диаметром суженной части d2 = 50 мм.
Определить, пренебрегая потерями энергии, расход воды Q по показанию ртутного дифманометра Δh = 3,8 см, подключенного к широкому и узкому сечению водомера.

|
Установить область сопротивления широкого и узкого участков водомера, если эквивалентная шероховатость Δэ = 0,1 мм.
Ответ: Q = 6,03 л/с.
Задача 3.26.По трубопроводу диаметром d1 = 200 мм с резким сужением до диаметра d2 = 100 мм перекачивают масло плотностью rм = 750 кг/м3. Избыточное давление в широкой трубе р1 = 176,6 кПа, а в узкой трубе р2 = 147,2 кПа. Геодезическая отметка первого сечения относительно второго z1 = +1 м.
Определить потери напора Δh1-2 на участке 1-2 при расходе масла Q = 31,4×10-3 м3/с.
Определить полную энергию потока в первом сечении (гидродинамический напор) Нгд и кинетическую Hv.
Ответ:Δh1-2 = 3,76 м; Нгд = 22,23 м; Hv = 0,051 м.
Задача 3.27.Трубопровод, имеющий в сечении 1 диаметр d1 = 150 мм, постепенно расширяется до диаметра d2 = 400 мм в сечении 2. Центр тяжести сечения 2 расположен выше центра тяжести сечения 1 на величину z2 = 2 м.
Определить разность полных напоров (Н1 – Н2) между сечениями 1 и 2, если расход воды по трубопроводу составляет Q = 106 л/с, а потери энергии на трение равны 20 % от потерь при внезапном расширении потока.
Ответ: Н1 – Н2 = 0,472 м.

|
Задача 3.28.По прямому трубопроводу постоянного диаметра d = 250 мм, с шероховатостью Δэ = 0,04 мм, длиной l = 250 м, наклоненному к горизонту под углом a = 0°55¢, подается вода с расходом Q = 49,1×10-3 м3/с.
Определить:
· давление воды р2 в сечении 2, если давление в сечении 1 составляет р1 = 196,2 кПа, а жидкость движется от сечения 1 к сечению 2;
· давление р2 при р1 = = 196,2 кПа, если жидкость движется от сечения 2 к сечению 1.
При расчетах проверка области сопротивления обязательна.
Ответ: р2 = 149031 Па; р2 = 164889 Па.
Задача 3.29.Вертикальная коническая труба длиной l = 4 м имеет нижний диаметр d1 = 500 мм и верхний d2 = 100 мм; из сечения 2-2 жидкость истекает в атмосферу со скоростью v2 = 10 м/с.

|
Определить:
· избыточное давление на входе воды в трубу р1;
· полную удельную энергию потока (с учетом атмосферного давления ра) на входе в трубу Нгд.1 и на выходе Нгд.2 относительно плоскости сравнения, проведенной через сечение 1-1.
Ответ: р1 = 93084 Па; Нгд.1 = 19,5 м; Нгд.2 = 19,1 м.
Задача 3.30.Определить гидравлический уклон I для напорного потока воды в трубе постоянного диаметра d = 0,1 м при расходе Q = 5×10-3 м3/с, если эквивалентная шероховатость трубы Δэ = 0,02 мм.
Ответ: I = 0,0043.
|
Задача 3.31.По новому трубопроводу постоянного диаметра d = 200 мм длиной l = 1,6 км перекачивают в сутки 2794 т тяжелой нефти (r = 924 кг/м3, ν = 1,4 Ст). Определить потери напора Δh по длине трубопровода, если он выполнен из стальных бесшовных труб.
Ответ: Δh » 8,36 м.
Задача 3.32.Определить допустимую высоту установки центробежного насоса над уровнем воды в колодце zн при следующих данных: вакуумметрическая высота всасывания насоса hвак = 4,8 м; диаметр всасывающей трубы d = 200 мм, ее длина l = 16 м; подача насоса Q = 173 м3/ч.
На всасывающем трубопроводе имеются местные сопротивления: фильтрующая сетка с обратным клапаном zс и два плавных колена (zк) с поворотом на 90° и радиусом закругления R = 200 мм.
При расчетах установление области сопротивления обязательно. Эквивалентную шероховатость трубы принять Δэ = 0,1 мм.
Ответ:zн < 3,9 м.
Задача 3.33.Определить диаметр нефтепровода d и режим движения Re нефти (r = 885 кг/м3, ν = 0,25 Ст), если скорость ее движения  при перекачке 600 т/сут и работе насоса по перекачке 8 ч/сут.
при перекачке 600 т/сут и работе насоса по перекачке 8 ч/сут.
Ответ: d = 158 мм; Re » 7600.
Задача 3.34.Из накопителя А в водоем В вода подается при температуре t = 30° С по сифонному трубопроводу с расходом Q = 50 л/с при разности уровней в водоемах Н = 2 м.
Трубопровод имеет местные сопротивления: сетчатый фильтр с обратным клапаном (zф » 5,5), два плавных колена с отношением r/R = 0,2 [1], шиберную задвижку с a/D = 0,5 [1] и выход в большую емкость; эквивалентная шероховатость Δэ = 0,065 мм.
Определить диаметр трубопровода d.
При решении использовать графический способ или метод последовательных приближений (итераций). Для определения параметров жидкости использовать рекомендации раздела 1.
Ответ: d = 192 мм.

|
Задача 3.35.Для условий задачи 3.34 проверить работу системы на отсутствие кавитации в опасном сечении (область второго пологого колена), до которого длина трубопровода составляет l = 40 м; высота b = 2м. Принять давление насыщенных паров воды (абсолютное) при t = 30° С рнп = 4214 Па и ра = 98100 Па.
Ответ: рmin.абс = 65,3 кПа > рнп, т.е. кавитации нет.
Задача 3.36.При какой скорости v осуществляется (теоретически) переход ламинарного режима в турбулентный, если жидкость движется в трубе диаметром d = 50 мм, а ее свойства соответствуют данным табл.1.5: бензин; вода; спирт; глицерин.
Ответ: v1 = 0,028 м/с; v2 = 0,047 м/с; v3 = 0,070 м/с; v4 = 40,37 м/с.
Задача 3.37. Определить диаметр d трубы длиной l = 10 м для прокачки по ней нефти (r = 885 кг/м3; n = 25×10-6 м2/с) с массовым расходом Qт = 600 т/сут при времени работы насоса Т = 8 ч/сут,, если потери напора составляют Δh = 0,03 м, а режим движения соответствует области гидравлически гладких труб.
Ответ: d = 224 мм.
Задача 3.38.Определить местную скорость v в точке А, отстоящей от стенки трубы на расстояние h = 12 мм, если движение жидкости ламинарное, диаметр трубы d = 0,1 м, расход жидкости Q = 18,5 л/с.
Ответ: v = 1,99 см/с.

|
Задача 3.39.В трубе диаметром d = 0,2 м на расстоянии h = 48 мм от стенки местная скорость масла и = 6,8 см/с. Определить суточный объемный расход Q масла, считая режим движения ламинарным.
Ответ: Q = 126 м3/сут.

 Задача 3.40.В самотечном трубопроводе диаметром d = 0,1 м течет нефть (условная вязкость 7,2° ВУ, r = 860 кг/м3) с массовым расходом Qт = 22 т/ч.
Задача 3.40.В самотечном трубопроводе диаметром d = 0,1 м течет нефть (условная вязкость 7,2° ВУ, r = 860 кг/м3) с массовым расходом Qт = 22 т/ч.
Определить режим движения нефти, если высота ее слоя в трубе h = 80 мм.
Ответ:Re = 2485.
Задача 3.41.Определить потерю напора Δh в трубопроводе длиной l = 500 м и диаметром d = 0,15 м при перекачке тяжелой нефти (r = 950 кг/м3; m = 1,33 П) с расходом Q = 20 л/с.
Ответ:Δh = 11,49 м.
Задача 3.42. Два резервуара с водой соединены между собой новой стальной сварной трубой с постоянным диаметром d = 50 мм, длиной l = 120 м.
Определить разность уровней воды Δh при постоянных отметках этих уровней во время движения воды по трубе при открытой задвижке ЗШ [1]; расход Q = 3 л/с. На трубе имеются местные сопротивления: задвижка, вход в трубу и выход из нее и два плавных колена с r/R = 0,5.
Установление области сопротивления обязательно.
Ответ:Δh » 7,55 м.
Задача 3.43.По трубопроводу диаметром D = 0,1 м, шероховатостью Δ = 0,15 мм и длиной l = 2850 м перекачивают жидкость с кинематическим коэффициентом вязкости n = 0,03 Ст при расходе Q = 9,5 л/с. Определить потерю напора Δh и приведенную длину трубопровода Lпр, если на нем имеются четыре полностью открытые шиберные задвижки, обратный клапан и диафрагма с диаметром отверстия d = 56 мм.
Ответ:Δh » 56 м; Lпр » 2885 м.

|
Задача 3.44.Определить критический расход (соответствующий теоретическому переходу ламинарного режима движения жидкости к турбулентному) воды Qв и керосина Qк, nк = 0,025 Ст при безнапорном движении жидкости по прямоугольному каналу шириной b = 1,2 м при слое жидкости в нем высотой h = 0,42 м.
Ответ: Q = 1,8 л/с; Q = 4,5 л/с.
Задача 3.45.Определить диаметр трубы d, имеющей шероховатость Δ = 0,1 мм и служащей для перепуска воды с расходом Q = 30 л/с из одного резервуара в другой при постоянной разности уровней в них Δh = 5 м и длине трубы L = 120 м.
Местными сопротивлениями пренебречь; использовать способ последовательных приближений.
Ответ: d » 128 мм.
Задача 3.46.Гидравлический уклон при движении воды по трубе с шероховатостью Δ = 0,1 мм составляет I = 0,01, средняя скорость потока v = 1,4 м/с.
Определить диаметр трубы d и расход воды Q.
Ответ: d = 185 мм; Q = 37,7 л/с.
Задача 3.47.Для потока жидкости прямоугольного сечения с площадью живого сечения S = 1,2 м2 найти такие размеры ширины потока b и высоты слоя жидкости h, чтобы гидравлический радиус Rг потока был наибольший.
Ответ: h = 0,775 м; b = 1,549 м; Rг.max = 0,387 м.
Задача 3.48.По шахтной вентиляционной трубе диаметром d = 500 мм, шероховатостью Δ = 0,2 мм проветривают тупиковую выработку длиной l = 120 м Определить избыточное давление р1, которое должен развить вентилятор при расходе воздуха (r = 1,186 кг/м3, n = 15,7×10-6 м2/с) в трубе Q = 220 м3/мин, если на выходе из трубы давление атмосферное.
Ответ: р1 > 84 Па.

|
Задача 3.49.Из бака А в бак Б следует перекачать поршневым насосом масло АМГ-10 (r = 850 кг/м3; ν = 10 сСт).
Определить допустимую по условиям отсутствия кавитации высоту [Н] расположения оси насоса над свободной поверхностью масла в баке А. Длина всасывающего трубопровода l = 6 м; скорость поршня vп = 0,8 м/с; диаметр поршня D = 70 мм, труб d = 32 мм; шероховатость труб Δ = 0,015 мм.
На трубопроводе имеются местные сопротивления: вход в трубу при выступающей в бак А трубе (zвх), пробковый кран при β = 0° (zкр, см. пример 3.2), две пары сочлененных по схеме (рис.3.2) плавных (R/r = 2) колен (zк) [1] и обратный клапан (zок = 2).
За опасное принять сечение к-к. Давление насыщенных паров рнп = 400 Па. Атмосферное давление ра = 98100 Па.
Ответ:[Н] < 2,77 м.
Задача 3.50.Для осушения скважины используют поршневой насос со скоростью поршня vп = 2 м/мин.
Проверить сечение к-к всасывающего вертикального трубопровода длиной l = 9,3 м, диаметром d = 32 мм на наличие кавитации, если воду следует поднять на высоту Н = 9 м при температуре t = 10 °С.
На трубе, кроме обычных сопротивлений, имеется обратный клапан (zок = 3). Диаметр поршня D = 70 мм.

|
Для определения параметров жидкости использовать рекомендации раздела 1.
Давление насыщенных паров воды при t = 10 °С рнп = 1200 Па. Принять атмосферное давление ра = 98100 Па.
Ответ: рк-к = 8550 Па. Кавитации нет.
Задача 3.51.От насоса N вода подается с давлением рн попеременно к гидромониторам М1 и М2, расположенным на разных горизонтах (z1 = z2 = 50 м). Один гидромонитор потребляет расход Q = 360 м3/ч. При этом потери давления в проточном тракте гидромонитора составляют Δрм = 1 ат.
Определить давление насоса р1н и р2н при следующих размерах трубопровода:
| Участок трубопровода | |||||
| Длина l, м | |||||
| Диаметр d, мм |
Принять шероховатость труб Δ = 0,22 мм. Трубопровод отнести к категории длинных.
Ответ: р1н » 123 ат; р2н » 133 ат.

|
Задача 3.52.В подготовительном забое вместо гидромониторов М1 или М2 применяют углепроходческий комбайн, на который подают воду (для организации самотечного гидротранспорта угля от забоя) с давлением р2 = 1 МПа; при этом в магистрали существует давление р1 = 12 МПа. Для снижения давления и расхода Q в линии на участке № 4 устанавливают диафрагму с диаметром отверстия d.
Определить диаметр диафрагмы d, если расход воды на комбайн Q = 0,05 м3/с, а диаметр труб магистрали D = 0,1 м.
Ответ: d = 26 мм.

|
Задача 3.53.При гидравлической добыче угля для подвода высоконапорной воды к гидромониторам используют для стыковки отрезков труб длиной l = 3 м быстроразъемные хомутовые соединения (БС), фланцы которых приварены с двух концов к каждому отрезку электродуговой сваркой с выступающей внутрь трубы высотой сварного шва на величину d » 1,5-2 мм.
Во сколько раз возрастут потери напора в трубе со сварными швами Δh¢ по сравнению с той же трубой, но без сварных швов Δh, если диаметр трубы d = 200 мм, а сопротивление труб без стыков при квадратичном законе сопротивления l = 0,0207?

|
Ответ:Dh¢/Dh = 1,058-1,092.
Задача 3.54.Поршень с четырьмя щелями перемещается под нагрузкой F вниз. Трансформаторное масло [1, с.314] из нижней полости цилиндра перетекает по щелям в его верхнюю полость.
Определить расход Q через щели поршня, режим движения масла в щелях, скорость vп движения поршня вниз и силу F.

|
Трением поршня и штока о стенки цилиндра и уровнями масла х1, х2 пренебречь. Для определения перепада давления на щели использовать формулу

где m – динамический коэффициент вязкости; d – характерный размер сечения щели.
Дано: r = 884 кг/м3; р1 = = 0,1 МПа; р2 = 0; l = 150 мм; а = 3 мм; b = 1,5 мм; D = 40 мм.
Ответ: Q = 10,6 л/мин; vп = 0,14 м/с; ламинарный режим; F = 12,8 кгс.
Дата добавления: 2015-04-18; просмотров: 1086; Мы поможем в написании вашей работы!; Нарушение авторских прав |