РАЗДЕЛ 2

ГИДРОСТАТИКА

Гидростатическое давление р – есть напряжение сжатия, возникающее от действия внешних сил F,

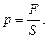
(2.1)

где S – площадь рассматриваемой поверхности, м².

Единицы измерения гидростатического давления: паскаль (Па), атмосфера (ат), килограмм-сила на сантиметр квадратный (кгс/см²), метры столба жидкости (м ст. ж.); последняя единица соответствует понятию «напор», который выражается через давление

(2.2)

Соотношение между различными единицами давления:

1 ат = 1 кгс/см² = 10 м вод. ст. = 736 мм рт. ст. = 98100 Па = = 98,1 кПа = 0,0981 МПа.

Согласно основному уравнению гидростатики давление в рассматриваемой точке жидкости (точка А на рис.2.1, а) есть алгебраическая сумма внешнего давления на жидкость и давления от столба жидкости над (или под) рассматриваемой точкой:

(2.3)

Различают: атмосферное давление р_а 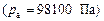, абсолютное давление p_абс, измеренное от абсолютного нуля; атмосферное давление абсолютное; избыточное положительное (кратко избыточное) давление или манометрическое р_и – избыток над атмосферным давлением; избыточное отрицательное давление или вакуумметрическое – недостаток до атмосферного давления.

Абсолютное давление всегда положительное, а вакуумметрическое не может быть больше атмосферного.

Внешнее давление р₀ может быть атмосферным, т.е. 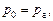и может отличаться от атмосферного.

Внешнее давление р₀ на жидкость может быть создано компрессором (+р_и) или вакуум-насосом (–р_и), а также силовым поршнем (рис.2.1, б).

Внешнее давление на жидкость р₀ передается во все ее точки без изменения (эффект Паскаля); на любой горизонтальной плоскости, проведенной через однородную жидкость в ее замкнутом объеме, давление одно и тоже. Объем считается замкнутым, если две его любые точки можно соединить непрерывной линией. На рис.2.1, в для однородной жидкости на горизонтальной плоскости N-N р₀ = const; линия р₀ – р₀ непрерывна. Эти признаки, в частности, используют при определении давления с помощью жидкостных приборов.

Относительный покой жидкости может соответствовать,например:

· движению сосуда с жидкостью по горизонтальной плоскости с ускорением a (рис.2.2) и тогда давление в точке А определяется по формуле

, (2.4)

где h – глубина погружения точки А (по вертикали) под поверхностью уровня с давлением , а угол a наклона свободной поверхности жидкости к горизонту определяется по формуле

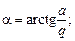(2.5)

· равномерному вращению сосуда с жидкостью с угловой скоростью w относительно вертикальной оси (рис.2.3). При этом уравнение свободной поверхности жидкости (параболоид вращения)

(2.6)

где r и z – цилиндрические координаты, вращающиеся вместе с сосудом; z₀ – вертикальная координата вершины параболоида от дна сосуда или иной заданной горизонтальной плоскости.

Высота параболоида при радиусе сосуда R

(2.7)

Начальное положение жидкости в сосуде (w = 0) соответствует плоскости N-N (рис.2.3). Давление p в любой точке на глубине h (например, в точке А) под свободной поверхностью с давлением p₀ определяется по уравнению (2.3).

Полная сила давления жидкости на плоскую фигуру (например, эллипс – в плоскости стенки сосуда, след которой в плоскости чертежа – линия АВ), наклоненную к горизонту под углом a, определяется по формуле (рис.2.4)

(2.8)

где h_ц – глубина погружения центра тяжести фигуры; l_ц – расстояние от свободной поверхности до центра тяжести, отсчитываемое в плоскости фигуры; S – площадь фигуры; p_ц – гидростатическое давление в центре тяжести фигуры.

Точка приложения силы F (центр давления Д) лежит ниже центра тяжести Ц и определяется по формуле:

(2.9)

где l_ц и l_д – соответственно расстояние по наклонной плоскости стенки от свободной поверхности до точек Ц и Д; I_ц – центральный момент инерции фигуры.

Для некоторых фигур (рис.2.5) силы от давления столба жидкости и координаты центра давления l_д даны в табл.2.1; все размеры даны в плоскости стенки АВ, которая изображена при a = 90°. Расположение фигуры ниже свободной поверхности жидкости отмечено координатой L. Для перехода к высотам h_ц и h_д следует воспользоваться связью вида h = lsina.

Таблица 2.1

Фигура	Вариант	S	Lц	lд	F
Прямо-угольник		ab
Прямо-угольник		ab
Треу-гольник
Треу-гольник
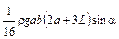
Трапеция
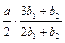
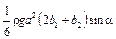
Круг		pr2

Для вертикальных фигур a = 90°, для горизонтальных фигур a = 0, .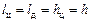

Силу давления жидкости F на плоские стенки с постоянной шириной b и центры давления l_д,h_д можно также определить графически с помощью эпюр давления [9]. При этом

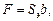(2.10)

где S_э – площадь эпюры давления.

Абсциссы эпюры давления выражают давление в соответствующих точках с учетом (или без учета).

В открытых резервуарах эпюра давления на прямоугольную стенку АВ есть прямоугольный треугольник АВС (рис.2.6) с основанием rgh и высотой h (или 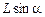– для наклонной стенки).

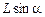В закрытых резервуарах при наличии избыточного давления на свободной поверхности искомая эпюра есть трапеция АВСД (рис.2.7) с основаниями: верхним р₀ и нижним и высотой h (или – для наклонной стенки).

Аналогичная эпюра будет и в случае открытого сосуда, но если при этом сила F определяется не на всю смоченную стенку АВС (рис.2.8), а только на ее нижнюю часть ВС.

Линия действия искомой силы F проходит через центр тяжести эпюры давления (точка О на рис.2.6, 2.7 и 2.8).

Центр давления также можно найти аналитически по формулам:

· для рис.2.7

; (2.11)

· для рис.2.8

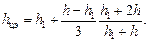(2.12)

При двухсторон­нем давлении жидкости на стенку центр тяжести О результирующей эпюры давления можно найти как графически, так и аналитически:

· результирую­щая сила от избыточного давления

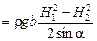; (2.13)

· плечо результирующей силы давления

(2.14)

Сила избыточного давления жидкости на криволинейные цилиндрические поверхности (рис.2.9) определяется по формуле

, (2.15)

где F_x – горизонтальная составляющая силы; F_z – вертикальная составляющая силы.

Составляющая F_x равна силе давления на вертикальную (плоскую) проекцию криволинейной поверхности. Составляющая F_z равна весу тела давления V.

Тело давления действительно (знак плюс, F_z направлена вниз), если находится в жидкости, и фиктивно (знак минус, F_z направлена вверх), если находится за пределами жидкости. Объем тела давления V – объем вертикального столба жидкости (действительного или фиктивного), опирающегося на заданную криволинейную поверхность и ограниченного сверху пьезометрической плоскостью.

На рис.2.9 стенка представлена четвертью кругового цилиндра радиусом r; на свободной поверхности атмосферное давление p_a; свободная поверхность в данном случае является пьезометрической плоскостью. Жидкость смачивает стенку снизу. Тело давления (в сечении – четверть круга) жидкости не принадлежит, следовательно, оно фиктивно (знак минус), а вертикальная составляющая силы F (F_z) направлена вверх.

Горизонтальная составляющая

, (2.16)

где b – длина поверхности вдоль оси OY; S = S_yoz – площадь проекции ADB на плоскость YOZ;

вертикальная составляющая

, (2.17)

где V – объем фиктивного тела давления, ; – площадь тела давления в плоскости XOZ,

Подставив найденные значения F_x и F_z в (2.15), найдем результирующую силу F. Составляющая F_x действует на плече (здесь h = r); направление равнодействующей F должно проходить через центр кривизны N; точка D есть точка приложения силы F.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 2.1. Найти силу , сжимающую тело Т до начала действия усилия и после его приложения .

Дано: F₁ = 120 Н; h = 20 см; S₁ = 0,01 м²; S₂ = 10 м²;

Трением и весом поршней пренебречь.

Решение. До момента приложения силы в точке А под большим поршнем действует давление от столба жидкости высотой h

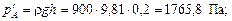
при этом тело Т испытывает силу

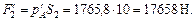
После приложения силы в точке А по закону Паскаля возникнет давление

при этом тело Т будет испытывать силу

Ответ:

Пример 2.2.Водоем частично перекрыт щитом, который находится в нижнем положении, оставляя свободным верхнее прямоугольное отверстие. По мере накопления воды в водоеме она начинает переливаться через верхнее отверстие в «сухую» часть канала и отводится по уклону канала от водоема. При необходимости щит переводят из нижнего положения в верхнее, при этом вода перетекает в канал через придонное отверстие.

Вертикальный щит шириной b перемещают с усилием Т в пазах с коэффициентом трения f. Вес щита G. Высота верхнего отверстия h₁, высота слоя воды в водоеме h.

Определить усилие Т и плечо приложения силы F от давления воды на щит в его нижнем положении если задано: f = 0,05; h₁ = 0,5 м; G = 2 кН; a = 90°; b = 2 м; h = 3,5 м;

Решение. Подъемное усилие

(2.18)

где F – сила давления воды на щит высотой h-h₁ и шириной b. Согласно табл.2.1 (вариант 2)

в обозначениях рисунка к примеру 2.2 (см. также рис.2.8)

Тогда искомое усилие

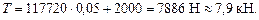
Плечо приложения силы F согласно табл.2.1 (вариант 2)

В обозначениях рисунка к примеру 2.2: a = h – h₁ = 3,5 – 0,5 = 3 м; L = h₁ = 0,5 м. Тогда

Замечание: плечо может быть найдено также графически.

Ответ:

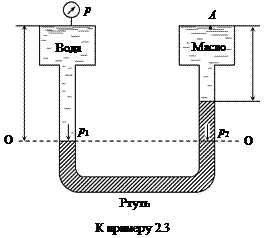
Пример 2.3. Определить вид и величину давления p_A в верхней точке правого сосуда, если в верхней точке левого сосуда манометрическое давление . Положение столбиков ртути в U-образной трубке относительно верхней точки сосудов: h₁ = 500 мм, h₂ = 400 мм. Относительная плотность масла .

Решение. Действительная плотность масла , где – плотность стандартного вещества, т.е. дистиллированной воды.

Манометрическое давление 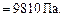Воспользуемся условием равновесия жидкости – проведем горизонтальную плоскость 0-0 по однородной жидкости (ртуть) в ее замкнутом объеме; при этом в левом (р₁) и правом (р₂) коленах трубки абсолютное давление будет одинаковым, т.е. р₁ = р₂.

Согласно основному уравнению гидростатики (2.3) абсолютное давление на плоскость 0-0 в левом колене и аналогично – в правом . Или, приравнивая правые части, имеем

Находим искомое давление

Полученный результат говорит о том, что в точке А имеет место отрицательное избыточное давление или вакуумметрическое.

Ответ: p_A = p_вак » 2,08 кПа.

Пример 2.4. Цилиндрический открытый сосуд с водой вращается вокруг вертикальной оси с постоянной угловой скоростью w. Диаметр сосуда D = 0,8 м.

Определить угловую скорость вращения w и число оборотов n сосуда, при которых глубина h воронки (высота параболоида вращения) была бы не более 0,9 м, а также линейную скорость v частиц воды у боковой поверхности сосуда и давление р_А в плоскости 0-0, расположенной ниже вершины параболоида на расстоянии z₀ = 0,2 м. Радиус расположения точки А r = 0,2 м.

;

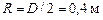
рад/с

и

об/мин.

При этом скорость частиц жидкости на радиусе R = 0,4 м v .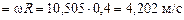

По формуле (2.6) расстояние точки А до свободной поверхности на радиусе r = 0,2 м

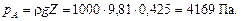
Ответ: w = 10,505 рад/с; n = 100 об/мин; v = 4,202 м/с; р_А = 4169 Па.

ЗАДАЧИ

Задача 2.1. Канал прямоугольного сечения шириной b = 3,5 м перегорожен щитом, который можно перемещать усилием T в вертикальных пазах боковых стен канала.

Определить графически и аналитически равнодействующую силу R от двухстороннего действия на щит воды и аналитически подъемное усилие Т, если коэффициент трения щита в пазах f = 0,35, вес щита G = 2,5 кН, уровни воды Н₁ = 4 м и Н₂ = 1,2 м.

Ответ: R ≈ 250 кН; Т ≈ 90 кН.

Задача 2.2. Вертикальный открытый цилиндрический сосуд радиусом R = 0,5 м и начальным слоем жидкости высотой h₀ = 1,5 м равномерно вращается со скоростью n = 100 об/мин.

Определить глубину воронки h₂ и минимальную высоту сосуда h₁, при которой жидкость не выливается из сосуда при его вращении.

Ответ: h₂ = 1,39 м; h₁ = 2,195 м.

Задача 2.3. Цилиндрический сосуд диаметром D = 0,4 м с горловиной диаметром d = 0,1 м заполнен водой на высоту h = 0,6 м. К поршню в горловине приложена сила F = 50 Н.

Определить силу F_д от манометрического давления на дно сосуда. Трением поршня о стенки горловины пренебречь.

Ответ: .

Задача 2.4. В открытом сосуде находится слой воды высотой 1,5 м и слой нефти высотой 4,2 м (р_н = 900 кг/м³).

Определить величину манометрического давления р_м на уровне дна сосуда.

Ответ: р_м = 0,528 ат.

Задача 2.5. Определить величину абсолютного давления p_абс на свободной поверхности жидкости в сосуде, если в пьезометре вода поднялась на высоту h = 1,8 м.

Ответ: p_абс = 115,76 кПа.

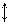
Задача 2.6. Определить разность давлений Dр в колбах А и В с водой, если разность уровней ртути в дифманометре Dh = 23 см. Разность уровней осей колб H = 1 м.

Ответ: Dр = 18507 Па.

Задача 2.7. Определить разность давлений ∆р в сечениях 1-1 и 2-2 газопровода, если разность уровней воды в коленах дифманометра ∆h = 24 см. Плотность газа ρ = 0,84 кг/м³.

Ответ:

Задача 2.8. Определить давление p₂ в сосуде В с воздухом, если в сосуде А с водой избыточное давление p₁ равно 2 ат, а разность уровней ртути в U-образной трубке, соединяющей сосуды, Dh = 1,6 м. Разность уровней сосудов H = 1 м, плотность ртути r = 13544 кг/м³.

Ответ: p₂ = 9119 Па.

Задача 2.9. В вертикальной скважине с глинистым раствором находится бурильный инструмент (буровая штанга, буровая коронка) массой m = 88 т. Определить нагрузку F на подъемное устройство, удерживающее (или поднимающее) буровой инструмент. Плотность глинистого раствора r_г = 1180 кг/м³, средняя плотность материала бурового инструмента r_б = 7850 кг/м³.

Ответ: F = 733513 Н.

Задача 2.10. Определить манометрическое давление воды в сосуде А при разности высот ртути в дифманометре h₂ = 25 см. Центр сосуда А расположен ниже линии раздела между водой и ртутью на расстоянии h₁ = 40 см.

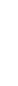Ответ: p_м = 37,278 кПа.

Задача 2.11. Определить разность высот ртути h₂ в дифманометре.

Центр сосуда А расположен на высоте h₁ = 0,4 м выше линии раздела между водой и ртутью. Манометрическое давление в сосуде А p_м = 37,278 кПа.

Ответ: h₂ = 0,309 м.

Задача 2.12. Центр сосуда А расположен ниже линии раздела между водой и ртутью на высоте h₁. Манометрическое давление в сосуде А p_м = 39,24 кПа; разность высот в дифманометре h₂ = 0,24 м.

Определить высоту h₁.

Ответ: h₁ = 0,736 м.

Задача 2.13. В трубопроводах А и В вода под давлением.

Разность высот ртути в дифманометре h = 0,2 м; плотность ртути ρ_р = 13600 кг/м³; плотность воды ρ_в = 1000 кг/м³.

Определить разность давлений Dр в трубопроводах А и В.

Ответ: Dр = 24,721 кПа.

Задача 2.14. На какой высоте Н над манометром М находится уровень нефти плотностью ρ_н = 840 кг/м³, если манометр показывает давление р_м = 1,21 ´ ´ 10⁵ Па, а на свободной поверхности нефти имеет место давление: 1) p_о.изб = 1 ат; 2) p₀ = p_а?

Ответ:1) H = 2,78 м; 2) H = 14,68 м.

Задача 2.15. При вращении открытого цилиндрического сосуда с водой с постоянной угловой скоростью w вода поднялась над дном сосуда на высоту H = 2 м.

Определить манометрическое давление р на дне: в центре сосуда p_о и через каждые 20 см от оси до стенки, а также расстояние Z₀ от дна сосуда до вершины параболоида (точка А).

Диаметр сосуда D = 1,2 м, число оборотов сосуда n = 60 об/мин.

Ответ: Z₀ = 1,276 м; р_о = 12521 Па; р₀₂ = 13310 Па; р₀₄ = 15676 Па; р₀₆ = 19620 Па.

Задача 2.16. Цилиндрический открытый сосуд заполнен водой на высоту h₀ = 0,24 м. Диаметр сосуда D = 0,6 м; высота сосуда H = 0,36 м.

Определить максимальные обороты n_max, при которых вода не будет выливаться из сосуда при его равномерном вращении.

Ответ: n_max = 69,1 об/мин.

Задача 2.17.Цистерна заполнена жидкостью до уровня h₀ = 2 м. Длина цистерны l = 20 м. Определить высоту H борта цистерны из условия отсутствия перелива через него жидкости при движении цистерны по горизонтали с ускорением а = 1,8 м/с².

Ответ: H ≥ 3,83 м.

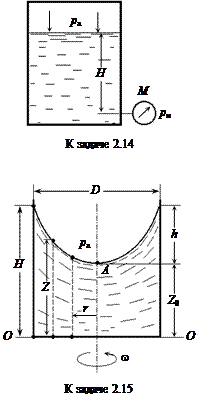
Задача 2.18. В покоящемся цилиндрическом сосуде диаметром D = 0,6 м находится вода c высотой слоя h_в = 0,8 м. Определить абсолютное гидростатическое давление p_aбc при вращении сосуда с частотой n = 90 об/мин для точек a, b, c, d, расположенных на окружностях радиусами соответственно r₁ = 0, r₂ = 0,1 м, r₃ = 0,2 м и r₄ = 0,3 м в плоскости a-d, отстоящей от дна сосуда на расстоянии Z = 0,4 м.

Ответ: p_aбc.a = 100028 Па; p_aбc.b = 100471 Па; p_aбc.с = = 101802 Па; p_aбc.d = 104021 Па.

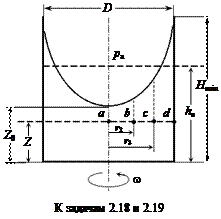
Задача 2.19. Цилиндрический сосуд диаметром D = 0,4 м с водой вращается с постоянным числом оборотов n = 150 об/мин; при этом вершина параболоида отстоит от дна сосуда на величину Z_о = 35 см.

Определить: 1) абсолютное давление p_aбc на дне сосуда в точках, расположенных на окружности радиуса соответственно 5, 10 и 20 см; 2) начальный уровень воды h_в до вращения сосуда; 3) минимальную высоту H_min сосуда, при которой жидкость не будет переливаться через его край.

Ответ: p_aбc.1 = 101842 Па; p_aбc.2 = 102766 Па; p_aбc.3 = 106462 Па; h_в = 0,602 м; H_min = 0,853 м.

Задача 2.20. Металлическая бочка массой m = 35 кг, диаметром D = 0,6 м и высотой H = 0,9 м заполнена водой и установлена на жестком основании А-А (первый вариант). Во втором варианте в крышке В-В выполнено отверстие диаметром d = 2 см и к нему присоединена вертикальная труба того же диаметра d высотой h = 15 м, заполненная водой. Масса трубы m = 1,65 кг.

Определить:

1) силу F₁ манометрического давления на дно бочки без трубы и силу G₁, передаваемую бочкой с водой на основание А-А;

2) силу F₂ манометрического давления на дно бочки с трубой и силу G₂, передаваемую в этом случае на основание А-А;

3) силу F₃ манометрического давления на крышку В-В.

Ответ: 1) F₁ = 2495 Н; G₁ = 2838 Н; 2) F₂ = 44080 Н; G₂ = 2900 Н; 3) F₃ = 41540 Н.

Задача 2.21. Две горизонтальные трубы диаметрами d₁ = 5 см и d₂ = 40 см соединены между собой; в этих трубах размещены поршни сечением соответственно S₁ и S₂, между которыми находится жидкость. С малой трубой соединена вертикальная трубка с водой высотой столба h = 0,8 м.

Какое усилие F₂ следует приложить к большому поршню, чтобы система находилась в равновесии, если к малому поршню приложено внешнее усилие F₁ = 98,1 Н? Трением поршней о стенки труб пренебречь.

Ответ: F₂ = 740,5 кг.

Задача 2.22. Открытый в атмосферу корытообразный резервуар полностью заполнен водой. Торцевые стенки резервуара – равнобокие трапеции с длиной основания l = 5 м и высотой h = 2 м; боковые стенки прямоугольной формы шириной b = 3 м наклонены к горизонту под углом a = 60°.

Определить силу манометрического давления на дно F₁, на боковую стенку F₂ и на торцевую стенку F₃.

Ответ: F₁ = 294,3 кН; F₂ = 68 кН; F₃ = 113,2 кН.

Задача 2.23. Для условий задачи 2.22 определить силу G, действующую на основание А-А. Собственный вес резервуара не учитывать.

Ответ: G = 36,22×10⁴ Н.

Задача 2.24. На плоский вертикальный прямоугольный затвор шириной b = 4 м, высотой H = 3,5 м и толщиной t = 0,08 м действует вода слева h₁ = 3 м и справа h₂ = 1,2 м. Затвор может перемещаться с силой Т в пазах при коэффициенте трения f = 0,5. Средний удельный вес материла затвора g_з = 1,18×10⁴ Н/м³.

Определить:

· равнодействующую силу R от двухстороннего давления воды на затвор;

· плечо l приложения силы R;

· начальное подъемное усилие Т.

Ответ: R = 148,33 кН; l = 1,114 м; T = 87,38 кН.

Задача 2.25. Определить результирующую силу R двухстороннего давления воды на плоский прямоугольный наклонный затвор, имеющий возможность поворачиваться относительно оси О под действием силы Т₁ или Т₂.

Ширина затвора b = 4 м, угол наклона к горизонту a = 60°, его вес G = 19620 Н. При расчете трением в шарнире О пренебречь. Сила Т₁ направлена перпендикулярно плоскости затвора, сила Т₂ – перпендикулярна дну канала.

Уровни воды: перед затвором h₁ = 3 м, за затвором h₂ = 1,2 м. Шарнир О расположен выше верхнего уровня на величину h = 0,8 м. Определить плечо l_д приложения силы R (центр давления) и силы Т₁, Т₂.

Ответ: R = 171,28 кН; l_д = 2,18 м; Т₁ = 125,95 кН; Т₂ = 251,9 кН.

Задача 2.26. Определить равнодействующую силу R от двухстороннего давления воды на плоский затвор, перекрывающий канал шириной b = 1 м, и плечо l приложения силы R, если задано: a = 45°, h₁ = 5 м, h₂ = 1,2 м, h = 3 м.

Ответ: R = 101 кН; l = 1,31 м.

Задача 2.27. Сила давления воды передается через обшивку плоского прямоугольного щита высотой H = 6 м и шириной В = 1 м на четыре горизонтальные балки. На каких расстояниях x от свободной поверхности следует расположить балки, чтобы они были нагружены одинаково?

Ответ: x₁ = 2 м; x₂ = 3,656 м; x₃ = 4,735 м; x₄ = 5,607 м.

Задача 2.28. Плоский прямоугольный затвор оперт шарнирно в точке О с возможностью поворота точки А по часовой стрелке и нагружен с двух сторон силами от давления воды.

Определить расстояние x от дна до оси вращения затвора О, чтобы при уровне воды слева от затвора H₁ ≥ 2 м затвор поворачивался автоматически, пропуская воду через образовавшуюся внизу щель. Высота слоя воды справа от затвора H₂ = 0,9 м.

Ответ: x = 0,76 м.

Задача 2.29.Призматический резервуар длиной l = 2,8 м, шириной b = 1,2 м и высотой h = 1,4 м заполнен жидкостью с удельным весом g = 7,456×10³ Н/м³. Определить силы манометрического давления на боковую F_б и торцевую F_т стенки резервуара и точки их приложения l_б и l_т (считая от свободной поверхности).

Ответ: F_б = 22,3 кН; F_т = 2,92 кН; l_б = 1,015 м; l_т = 0,7 м.

Задача 2.30. Вертикальный щит перегораживает канал трапецеидального сечения. Глубина воды в канале Н = 1,4 м, ширина канала по дну b = 1,6 м, по свободной поверхности В = 3,5 м.

Определить силу F давления воды на щит и точку ее приложения h_д.

Ответ: F = 21,46 кН; h_д = 0,867 м.

Задача 2.31. Вертикальный плоский прямоугольный щит, состоящий из пяти одинаковых досок шириной а = 20 см и длиной l = 1,6 м, сдерживает подпор воды высотой H = 1 м.

Определить силу F давления воды на щит в целом и на каждую доску щита в отдельности.

Ответ: F = 7848 Н; F₁ = 314 Н; F₂ = = 942 Н; F₃ = 1570 Н; F₄ = 2197 Н; F₅ = 2825 Н.

Задача 2.32. Определить силу F давления воды на стенку треугольной формы, обращенную вершиной вниз, если уровень воды перед стенкой H = 1,2 м, а угол при вершине a = 90°.

Ответ: F = 5650 Н.

Задача 2.33. Плоский прямоугольный затвор шириной а = 0,4 м и высотой h = 0,3 м может поворачиваться вокруг оси О, перпендикулярной к плоскости рисунка, в указанном направлении. Определить вес груза G на конце рычага длиной l_G = 0,6 м, жестко прикрепленного к затвору, чтобы последний автоматически открывал сток воды при ее уровне H = 1,4 м.

Ответ: G = 382,6 Н.

Задача 2.34. Определить силу F давления нефти плотностью r_н = 836 кг/м³ на крышку бокового люка и координату центра давления h_д, если уровень нефти над центром тяжести крышки H = 8 м, а диаметр крышки d = 0,4 м.

Ответ: F = 8,24 кН; h_д = 8,00125 м.

Задача 2.35. Определить толщину d стенки стального трубопровода с внутренним диаметром d = 0,2 м, предназначенного для перекачки жидкости под давлением р = 35×10⁵ Па, если допустимое напряжение на растяжение для материала трубы (Ст.3) составляет [s]_р = 10⁸ Па.

Ответ: d = 3,5 мм.

Задача 2.36. Определить силу F давления воды на цилиндрическую поверхность АВ с центральным углом a = 60°, если высота слоя воды перед ней H = 6 м, а ширина этой поверхности b = 10 м.

Ответ: F = 2,28×10⁶ Н.

Задача 2.37. Вертикальный цилиндрический резервуар высотой H = 6,2 м и диаметром D = 17 м полностью наполнен водой. Определить силу F давления воды на боковую стенку.

Ответ: F = 3,2×10⁶ Н.

Задача 2.38. Определить силу F давления жидкости плотностью r = 946 кг/м³ на 1/4 часть цилиндрической поверхности радиусом R = 3 м и шириной b = 6 м.

Ответ: F = 466 кН.

Задача 2.39. В вертикальном цилиндрическом резервуаре диаметром D = 8 м находится вода высотой слоя h₁ = 1,2 м и нефть плотностью r_н = 900 кг/м³ и высотой слоя h₂ = 6,6 м. Определить манометрическое давление р у дна резервуара и силу F действия жидкости на дно.

Ответ: р = 0,7×10⁵ Па; F = 3600 кН.

Задача 2.40. Определить равнодействующую силу F двухстороннего давления воды на плоскую стенку шириной b = 1,5 м, если ее наклон к горизонту составляет угол a = 45°. Уровень воды перед стенкой H₁ = 6 м, за стенкой H₂ = 2 м.

Ответ: R = 333013 Н.

Задача 2.41. Поверхность АВС, представляющая собой половину кругового цилиндра (цилиндрического затвора) диаметром D = 3 м и шириной b = 10 м, подвержена одностороннему давлению воды слоем H = 4,2 м, находящейся в открытом резервуаре.

Определить силу F манометрического давления на затвор и центр давления h_д.

Ответ: F = 867 кН; h_д = 2,98 м.

Задача 2.42. Определить толщину d стенок стального трубопровода с внутренним диаметром D = 0,6 м, находящегося под средним гидростатическим давлением р = 2,943 МН/м². Допустимое напряжение на растяжение материала трубы составляет [s] = 137,34 МН/м².

Ответ: d = 6,4 мм.

Задача 2.43. Определить разность уровней h воды под колоколом и в резервуаре. Масса колокола m = 2990 кг, его диаметр D = 4,2 м. Толщиной стенок колокола пренебречь.

Ответ: h = 0,216 м.

Задача 2.44. Нефтеналивное судно прямоугольного сечения с плоским дном длиной l = 100 м и шириной b = 20 м с полным грузом имеет осадку h₁ = 2,5 м, а без груза h₂ = 0,4 м. Определить массу нефти m_н, перевозимой судном. Плотность воды принять r_в = 1000 кг/м³.

Ответ: m_н = 4200 т.

Задача 2.45. Плотность жидкости r_ж измеряется ареометром, диаметр внешней трубки которого d = 20 мм, диаметр колбы с дробью D = 30 мм, а масса ареометра m_а = 0,054 кг. Определить r_ж и ориентировочно вид жидкости (см. табл.1.1), если глубина погружения ареометра составила H = 0,15 м.

Ответ: r_ж = 882 кг/м³, жидкость – минеральное масло.

Задача 2.46. Для определения плотности r_с неизвестного сплава его слиток взвесили на пружинных весах дважды: один раз в воздухе, второй раз – погрузив его в воду. Вес слитка в воздухе G = 7400 Н, в воде G = 1586 Н. Определить плотность сплава r_с.

Ответ: r_с = 1273 кг/м³.

Задача 2.47. Деревянный призматический брус длиной l, шириной b, высотой h = 0,3 м лежит в воде плоскостью l ´ b с погружением H; плотность дерева бруса r_д = 716 кг/м³. Определить глубину погружения бруса Н.

Ответ: Н = 0,215 м.

Задача 2.48. Определить вес G труб общей длиной L = 2,9 км, опущенных в скважину, заполненную глинистым раствором плотностью ρ_г = 1630 кг/м³, если известно, что 1 м таких труб с муфтами в воздухе весит 300 Н. Плотность материала труб r_т = 7500 кг/м³.

Ответ: G = 680,9 кН.

Задача 2.49. Определить силу F₁ на рычаге длиной а = 1 м, если прессуемое тело А должно быть сжато силой F₂ = 156,96 кН.

Диаметры малого поршня d = 2,5 см, большого D = 25 см; малое плечо рычага b = 0,1 м. Трением поршней и их весом пренебречь.

Ответ: F₁ = 156,96 Н.

Задача 2.50. Определить давление р, создаваемое гидравлическим грузовым аккумулятором, и запасенную им энергию Э, если вес его движущихся частей G = 725,94 кН, диаметр плунжера D = 0,2 м, ход плунжера H = 6 м и полный КПД аккумулятора η = 0,85.

Ответ: р = 19,65 МПа; Э = 3,7 МДж.

Задача 2.51. Определить полезную нагрузку F, действующую вдоль штока, если в поршневую полость гидроцилиндра подводится манометрическое давление р₁ = 7,848×10⁵ Па, а в штоковой полости существует противодавление (манометрическое) р₂ = = 0,981×10⁵ Па. Диаметры поршня D = 10 см, штока d = 3 см. Трением пренебречь.

Ответ: F = 5460 Н.

Задача 2.52. Определить удельный вес g_б деревянного бруса длиной l = 1 м, шириной b = 0,3 м и высотой Н = 0,2 м, плавающего в воде с осадкой h = 16 см.

Ответ: g_б = 7848 Н/м₃.

Задача 2.53. Прямоугольная баржа длиной l = 18 м и шириной b = 9 м загружена песком ровным слоем h. Осадка баржи с песком H = 0,5 м. Определить объем песка V_п, если его относительная плотность d = 2, и высоту слоя песка h. Массу баржи не учитывать.

Ответ: V_п = 40,5 м³; h = 0,25 м.

Задача 2.54. Деревянный брус длиной l = 5 м, высотой h = 0,3 м и шириной b = 0,3 м плавает в воде с осадкой H.

Определить осадку Н бруса, если относительная плотность его материала d = 0,7.

Определить, сколько человек (n) средней массой m = 67,5 кг могут встать на этот брус, чтобы его осадка составила Н = h = 0,3 м.

Ответ: Н = 0,21 м; n = 2.

Задача 2.55. Объемное водоизмещение подводной лодки V = 600 м³. Для погружения лодки ее отсеки были заполнены морской водой в количестве ΔV = 80 м³. Относительная плотность морской воды d = 1,025. Определить, какая часть объема лодки V_погр будет погружена в воду при ΔV = 0 и чему равен вес лодки G_л при ΔV = 0.

Ответ: G_л = 522,9×10⁴ Н; V_погр/V = 0,867.

Задача 2.56. В горизонтальный закрытый металлический бак призматической формы длиной l = 4 м, имеющий в вертикальном сечении равносторонний треугольник со сторонами а = 1,2 м, налит керосин (g_к = 7456 Н/м³) высотой слоя h. Все стенки бака имеют толщину d = 5 мм; относительная плотность металла . Бак с керосином плавает в воде с осадкой H = 0,8 м. Определить высоту слоя керосина h.

Ответ: h = 0,747 м.

Задача 2.57. Определить количество бревен n₁, из которых нужно сколотить плот, чтобы перевезти груз весом G_г = 2550 Н. Диаметр бревен d = 16 см, их длина L = 7 м. Осадка плота Н составляет 0,13 м. Массу перевозчика принять m = 75 кг, а относительную плотность намокших бревен . Какое количество n₂ бревен понадобится, если их верх (верх плота) будет заподлицо со свободной поверхностью воды?

Ответ: n₁ ≈ 20 шт; n₂ ≈ 10 шт.

Задача 2.58. Определить, при каком манометрическом давлении воды р внутри водопроводной трубы откроется клапан K, закрывающий при горизонтальном положении рычага выходное отверстие трубы, если плечо b в шесть раз больше плеча а. Диаметр трубы d = 5 см, а диаметр полого поплавка (шара) D = 20 см. Весом поплавка и рычага пренебречь.

Ответ: р = 1,256×10⁵ Па.