Задачи оптимизации производства

Основные понятия

Изокванта – совокупность сочетаний ресурсов, при которых может быть произведено определенное количество продукции.

Доходом (выручкой) фирмы в определенном периоде называется произведение общего объема выпуска продукции на рыночную стоимость этой продукции:

R= 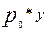y=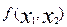

R- доход

- цена продукции

y-объем выпуска.

Издержками фирмы называют общие выплаты в определенный временной период за все виды затрат:

- объемы используемых фирмой ресурсов (факторов производства)

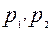- рыночные цены на эти ресурсы.

Прибыль – разность между полученным фирмой доходом R и издержками C^

В теории фирмы принято считать, что если фирма функционирует в условиях чистой совершенной конкуренции, то на рыночные цены , , 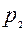она влиять не может, то есть фирма с ними соглашается.

Тогда основная цель фирмы заключается в том, чтобы максимизировать прибыль путем рационального распределения используемых ресурсов.

Формально задача максимизации прибыли в определенном временном периоде имеет вид:

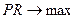
Такая постановка задачи зависит от того, какой временной период (долговременный или кратковременный) предшествует периоду, в котором фирма максимизирует свою прибыль.

В случае долговременного промежутка фирма может свободно выбирать любой вектор затрат 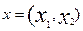из пространства затрат. Поэтому задача максимизации прибыли в случае долговременного промежутка имеет следующий вид:

при .

Задача максимизации прибыли в случае долговременного промежутка представляет собой задачу на абсолютный глобальный максимум при . Эта задача имеет единственное решение в точке, которая называется локальным (частичным) рыночным равновесием фирмы.

Графически решение данной задачи будет в точке, где изокванта касается изокосты.

В случае кратковременного промежутка фирма должна учитывать неизбежные лимиты на объемы используемых ресурсов. Формально это можно записать в виде неравенства:

Таких ограничений может быть несколько, следовательно, задача максимизации прибыли для кратковременного промежутка имеет вид задачи математического программирования:

при и .

Данная задача имеет единственное решение в точке, где изокванта и изокоста пересекаются, а не касаются. При этом изокоста соответствует большим издержкам, чем в долгосрочном периоде.

Линия уровня функции издержек производства называется изокостой. В связи с тем, что по экономическому смыслу , изокоста есть отрезок прямой, попадающей в неотрицательный октант плоскости :

Отрезок, расположенный северо-восточнее начала координат, соответствует большим издержкам производства.