КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интерференция волн. Стоячие волны
Интерференцией волн называется явление наложения волн, при котором происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других в зависимости от соотношения между фазами этих волн. Интерферировать могут только когерентные волны, которым соответствуют колебания, совершающиеся вдоль одного и того же или близких направлений.
 |
Две волновых процесса называются когерентными, если они согласованно протекают в пространстве и времени. Две монохроматические волны называются когерентными, если равны их частоты, т.е. разность их фаз не зависит от времени. Синусоидальные волны, частоты которых одинаковы, когерентны всегда.
Рассмотрим два точечных источника S1 и S2, которые испускают сферические волны с одинаковой амплитудой А0 и с постоянной разностью фаз (рис. 17.3.):
 |
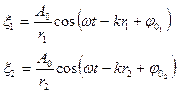где r1 и r2 - расстояния от источников волн до рассматриваемой точки М; k – волновое число; φ01 и φ02 – начальные фазы двух сферических волн соответственно.
По принципу суперпозиции, результирующее колебание в точке М описывается формулой
ξ=ξ1+ξ2=Асоsφ
где А – амплитуда результирующего колебания, φ – фаза результирующего колебания. Для нахождения А и φ воспользуемся методом векторных диаграмм (рис.16.4).
 |
Из рисунка амплитуда результирующей волны
 |
где амплитуды волн
Так как для двух когерентных источников φ1 –φ2=const, то результат интерференции двух волн зависит от величины (r2-r1), называемой геометрической разностью хода.
интерференционный максимум
 |
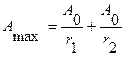наблюдается в точках, где 
, m- любые целые числа (0,1,2,3,…..), называемые порядком интерференционного максимума
Волновое число k связано с длиной волны по формуле
С учетом этого условие интерференционного максимума:
 |
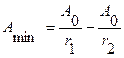Амплитуда результирующего колебания минимальна
в точках, где
Волновое число k связано с длиной волны по формуле
С учетом этого условие интерференционного минимума:
Интерференция волн приводит к перераспределению энергии колебаний между соседними областями среды. Однако в среднем для большой области пространства энергия результирующей волны равна сумме энергий интерферирующих волн. Этот результат — следствие закона сохранения и превращения энергии.
Дата добавления: 2015-02-09; просмотров: 183; Мы поможем в написании вашей работы!; Нарушение авторских прав |