Дифференциальное уравнение электромагнитных волн. Энергия электромагнитных волн. Вектор Умова - Пойтинга.

Электромагнитными волнами называются возмущения электромагнитного поля (т.е. переменное электромагнитное поле), распространяющееся в пространстве. Утверждение о существовании электромагнитных волн является непосредственным следствием уравнений Максвелла.

Если среда представляет собой однородный диэлектрик, не обладающий сегнетоэлектрическими и ферромагнитными свойствами, то , где ε, μ – постоянные скалярные величины, не зависящие ни от координат, ни от времени.

В этом случае уравнения Максвелла можно записать в виде:

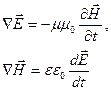
Продифференцировав первое уравнение по координатам, получим следующее равенство с учетом второго уравнения:

где - оператор Лапласа

учитывая, что получим

Если сравнить полученное выражение с общим волновым уравнением

,

то можно сделать вывод, что .

Откуда фазовая скорость электромагнитных волн

.

В вакууме (т.е. при ε=μ=1) скорость электромагнитных волн совпадает со скоростью света в пустоте с.

Следствием теории Максвелла является поперечность электромагнитных волн: векторы поля волны лежат в плоскости, перпендикулярной к направлению распространения волны, т.е. к вектору ее скорости в рассматриваемой точке поля.

Из уравнений Максвелла следует, что в электромагнитной волне векторы всегда колеблются в одинаковых фазах, причем мгновенные значения Е и Н в любой точке связаны соотношением

Таким образом, Е и Н одновременно достигают максимума, одновременно обращаются в нуль и т.д. Следовательно, дифференциальные уравнения электромагнитных волн будут иметь вид

(17.7.1)

Уравнения (17.7.1) называются уравнениями плоских монохроматических волн, где Е_0у , Н_0у – амплитудные значения напряженности электрического и магнитного полей волны.