КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Стоячие волны
Частным случаем интерференции волн являются стоячие волны.
Стоячей волной называется волна, образующаяся в результате наложения двух бегущих синусоидальных волн, которые распространяются навстречу друг другу и имеют одинаковые частоты и амплитуды. Стоячая волна образуется, например, пи отражении от преград. Падающая на преграду волна и бегущая ей навстречу отраженная волна, налагаясь друг на друга, дают стоячую волну.
 |
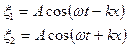Пусть две плоские волны с одинаковыми амплитудами и частотами распространяются навстречу друг другу вдоль х:
Сложив вместе эти уравнения и преобразовав результат по формуле для суммы косинусов
получим уравнение результирующего колебания двух плоских волн (уравнение стоячей волны)
(17.6.1)
В точках, координаты которых удовлетворяют условию
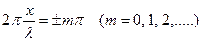(17.6.2)
 |
амплитуда колебаний достигает максимального значения (т.к.
). Точки среды, в которой амплитуда достигает своего максимального значения, называется пучностями стоячей волны.
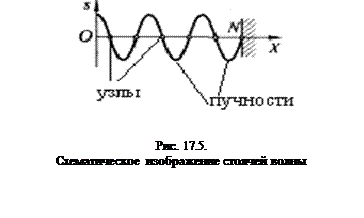
На рис. 17.5. представлен характер движения различных точек натянутой упругой нити при установившейся в ней поперечной стоячей волне.
Из условия (17.6.2) следует, что координата пучности
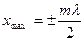(17.6.3)
При этом следует иметь в виду, что пучность представляет собой не отдельную точку, а плоскость, точки которой имеют значения, определяемые формулой (17.6.3).
В точках координаты, которых удовлетворяют условию
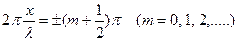(17.6.4)
амплитуда колебаний равна нулю (т.к.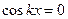 
). Точки среды, в которой амплитуда достигает своего минимального значения, называется узлами стоячей волны (рис.17.5).
Из условия (17.6.4) следует, что координата узла стоячей волны
(17.6.5)
Узел, так же как и пучность представляет собой не одну точку, а плоскость, точки которой имеют значения координаты, определяющие формулой (17.6.5).
Расстояния между двумя соседними узлами и между двумя соседними пучностями одинаковы и равны половине длины бегущих волн. Эту величину называют длиной стоячей волны: λСТ = λ/2.
В таблице 1 приведен сравнительный анализ основных характеристик бегущей и стоячей волн.
Таблица 1.
| Бегущая волна | Стоячая волна |
| Амплитуда колебаний | |
| Все точки волны совершают колебания с одинаковой амплитудой | Все точки между двумя узлами колеблются с разными амплитудами |
| Фаза колебаний | |
| зависит от координаты х рассматриваемой точки | Все точки между узлами колеблются с одинаковыми фазами |
| При переходе через узел фаза колебаний изменяется на π; Точки лежащие по разные стороны от узла колеблются в противофазе | |
| Перенос энергии | |
| Энергия колебательного движения переносится в направлении распространения бегущей волны | Переноса энергии нет, лишь в пределах λ/2 происходит взаимные превращения кинетической энергии в потенциальную и обратно |
Образование стоячих волн наблюдается при интерференции бегущей и отраженной волн. Если среда, от которой происходит отражение, менее плотная, то на границе сред образуется пучность. Если среда, от которой происходит отражение, более плотная, то на границе сред образуется узел стоячей волны.
Дата добавления: 2015-02-09; просмотров: 294; Мы поможем в написании вашей работы!; Нарушение авторских прав |