Упражнения к Глава 4

4.1.Вычислите пределы функций.

1) 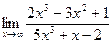;	2) ;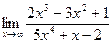
3) ;	4) ;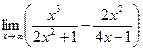
5) 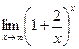;	6) ;
7) 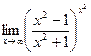;	8) ;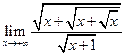
9) 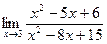;	10) ;
11) 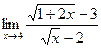;	12) ;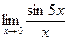
13) 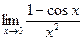;	14) ;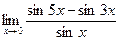
15) 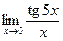;	16) ;
17) 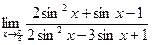;	18) ;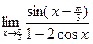
19) 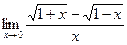;	20) .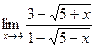

4.2.Найдите горизонтальные и вертикальные асимптоты графиков функций.

1) ;	2) ;
3) .

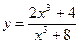4.3.Найдите наклонные и вертикальные асимптоты графиков функций.

1) 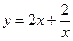;	2) ;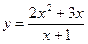
3) .

4.4.Придумайте примеры функций (в каждом случае запишите аналитическое выражение и постройте график):

1) с заданными вертикальными асимптотами ; ; ;

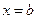2) с заданными горизонтальными асимптотами ; ;

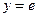3) с заданной наклонной асимптотой ;

4) с различными комбинациями асимптот видов, упомянутых в пунктах 1)-3).

4.5.Докажите, что функция 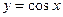непрерывна при всех действительных .

4.6.Докажите, что функция 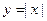непрерывна.

4.7.Исследовать на непрерывность следующие функции:

1) 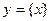;	2) ;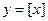
3) 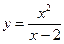;	4) ;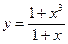
5) 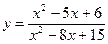;	6) ;
7) 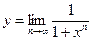, 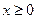;	8) .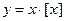

Для каждой из функций построить график.

4.8.Приведите пример всюду разрывной функции.

4.9.Функции 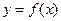и 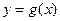разрывны при . Можно ли утверждать, что функция 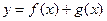также разрывна при ?

4.10.Функция 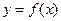непрерывна в точке 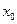, а функция 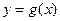разрывна в точке 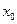. Может ли функция 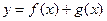быть непрерывной в этой точке?

4.11.Функция 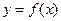непрерывна в точке 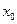, а функция 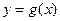разрывна в этой точке. Можно ли утверждать, что функция 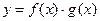разрывна при ?

4.12.Функции 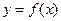и 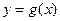разрывны в точке . Можно ли утверждать, что функция 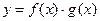также разрывна в этой точке?

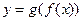4.13.Исследуйте на непрерывность функции и , где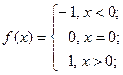

1) ;	2) ;
3) ;	4) .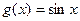

4.14.Докажите, что любой многочлен 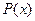нечетной степени имеет хотя бы один действительный корень.