
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
II. (Теорема Больцано-Вейерштрасса).
Если функция 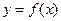 непрерывна на отрезке
непрерывна на отрезке 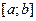 и её значения на концах отрезка имеют различные знаки, то найдется точка
и её значения на концах отрезка имеют различные знаки, то найдется точка 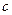 на отрезке
на отрезке 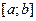 , в которой
, в которой  обращается в нуль.
обращается в нуль.
Доказательство:(теоремы Больцано-Вейерштрасса)
Разделим отрезок 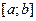 пополам точкой
пополам точкой 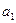 . Если
. Если 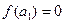 , то теорема доказана. Если же
, то теорема доказана. Если же 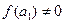 , то на одной из половин
, то на одной из половин 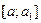 или
или 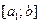 функция
функция 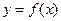 принимает на концах значения различных знаков. Пусть для определенности
принимает на концах значения различных знаков. Пусть для определенности 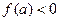 ,
, 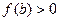 ,
, 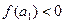 , тогда такой половиной будет отрезок
, тогда такой половиной будет отрезок 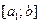 . Этот отрезок снова разделим пополам точкой
. Этот отрезок снова разделим пополам точкой 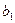 и повторим проведенное рассуждение. В результате либо мы найдем точку, в которой
и повторим проведенное рассуждение. В результате либо мы найдем точку, в которой  обращается в нуль, либо получим стягивающуюся систему отрезков
обращается в нуль, либо получим стягивающуюся систему отрезков 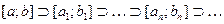 (1) с таким свойством: в точках
(1) с таким свойством: в точках 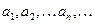 функция
функция  отрицательна, а в точках
отрицательна, а в точках 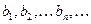 - положительна.
- положительна.
По теореме 6 о стягивающейся системе отрезков найдется точка 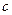 , общая для всех отрезков системы (1):
, общая для всех отрезков системы (1):  . Покажем, что в этой точке функция
. Покажем, что в этой точке функция 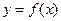 обращается в нуль. Предположим, что
обращается в нуль. Предположим, что 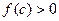 , но
, но 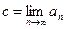 и с одной стороны
и с одной стороны 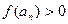 для
для 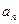 из
из 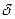 -окрестности точки
-окрестности точки 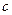 (по лемме), а с другой стороны
(по лемме), а с другой стороны 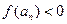 по условию. Полученное противоречие доказывает, что
по условию. Полученное противоречие доказывает, что 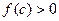 невозможно. Аналогично доказывается, что
невозможно. Аналогично доказывается, что 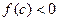 невозможно. Отсюда делаем вывод, что
невозможно. Отсюда делаем вывод, что 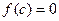 .
.
Дата добавления: 2014-11-13; просмотров: 306; Мы поможем в написании вашей работы!; Нарушение авторских прав |