
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Классификация точек разрыва разрывных функций
Рассмотрим графики функций:  (Рис. 36),
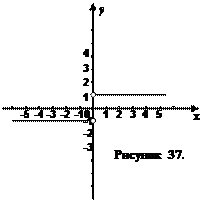
(Рис. 36),  (Рис. 37),
(Рис. 37), 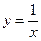 (Рис. 38). Мы видим, что в каждом случае график функции состоит из двух кусков, значит, рассматриваемые функции не являются непрерывными.
(Рис. 38). Мы видим, что в каждом случае график функции состоит из двух кусков, значит, рассматриваемые функции не являются непрерывными.
Определение 75.
 |

 |
Точкой разрыва функции
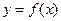 называют точку
называют точку  , в которой эта функция не является непрерывной.
, в которой эта функция не является непрерывной.
Таким образом,  - точка разрыва функции
- точка разрыва функции  ;
;  - точка разрыва функции
- точка разрыва функции  и
и  - точка разрыва функции
- точка разрыва функции 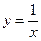 .
.
Но характер разрывов в этих трех случаях существенно отличается друг от друга. Действительно, хотя функция  - не определена в точке
- не определена в точке  , но существуют оба односторонних предела при
, но существуют оба односторонних предела при  и они равны между собой. Легко устранить такой разрыв, доопределив функцию так:
и они равны между собой. Легко устранить такой разрыв, доопределив функцию так:  .
.
Определение 76.Точка  называется точкой разрыва I рода (разрыв функции
называется точкой разрыва I рода (разрыв функции 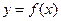 устранимый), если в этой точке существуют оба односторонних предела и они равны между собой:
устранимый), если в этой точке существуют оба односторонних предела и они равны между собой:  .
.
Определена ли функция в этой точке – не важно, но если определена, то значение функции в этой точке не совпадает с пределом функции в этой точке.
Функция  (рис. 37), не определенная при
(рис. 37), не определенная при  , имеет оба односторонних предела при
, имеет оба односторонних предела при 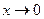
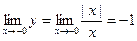 ;
;  . Как видно, они не равны между собой. Такой разрыв устранить невозможно.
. Как видно, они не равны между собой. Такой разрыв устранить невозможно.
Определение 77.Точка  называется точкой разрыва I рода (разрыв неустранимый) функции
называется точкой разрыва I рода (разрыв неустранимый) функции 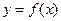 , если в этой точке существуют оба односторонних предела, но они не равны между собой
, если в этой точке существуют оба односторонних предела, но они не равны между собой  .
.
Определение 78.Разность  называется скачком функции и обозначается буквой
называется скачком функции и обозначается буквой  .
.
Таким образом, если в точке  разрывная функция
разрывная функция 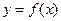 имеет конечный скачок
имеет конечный скачок  , то в этой точке функция имеет разрыв I рода; разрыв является устранимым, если
, то в этой точке функция имеет разрыв I рода; разрыв является устранимым, если  , и неустранимым в противном случае.
, и неустранимым в противном случае.
Функция  имеет в точке
имеет в точке  разрыв I рода, неустранимый, скачок
разрыв I рода, неустранимый, скачок  .
.
Определение 79.Точка  называется точкой разрыва II рода функции
называется точкой разрыва II рода функции 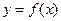 , если в этой точке не существует хотя бы один из односторонних пределов.
, если в этой точке не существует хотя бы один из односторонних пределов.
Пример 84.Функция 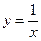 при
при  не имеет предела ни слева:
не имеет предела ни слева: 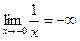 , ни справа
, ни справа  , поэтому
, поэтому  - точка разрыва II рода функции
- точка разрыва II рода функции 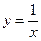 .
.
Пример 85.Функция 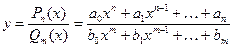 непрерывна при всех
непрерывна при всех  , при которых
, при которых  , если
, если  - простой корень многочлена
- простой корень многочлена 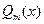 , но
, но 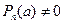 , то
, то  - точка разрыва II рода функции
- точка разрыва II рода функции 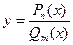 , а если
, а если  , то
, то  - точка разрыва I рода (разрыв устранимый).
- точка разрыва I рода (разрыв устранимый).
Функция может иметь разрыв и в случае, когда она задается на разных участках разными аналитическими выражениями. В этом случае «точки стыка» могут быть точками нарушения непрерывности.
Пример 86.Функция 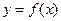 задана следующим образом
задана следующим образом  . Исследовать эту функцию на непрерывность.
. Исследовать эту функцию на непрерывность.
Решение. Функция  - непрерывна при
- непрерывна при  , функция
, функция  непрерывна при
непрерывна при 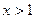 . В точке
. В точке  функция не определена, но
функция не определена, но  ;
;  . Значит, эта функция разрывная при
. Значит, эта функция разрывная при  , точка разрыва I рода, разрыв неустранимый, скачок
, точка разрыва I рода, разрыв неустранимый, скачок  .
.
Отметим, что точки разрыва II рода часто связаны с вертикальными асимптотами для графика функции 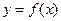 .
.
Пример 87.Исследовать на непрерывность функцию  и схематически построить ее график.
и схематически построить ее график.
Решение: рассмотрим  ; функция разрывна при
; функция разрывна при  и при
и при  .
.
 |
При

 ; в этой точке разрыв I рода, устранимый.
; в этой точке разрыв I рода, устранимый.
При 
 - не существует, значит, в этой точке разрыв II рода.
- не существует, значит, в этой точке разрыв II рода.
Рассмотрим функцию  ; она имеет горизонтальную асимптоту
; она имеет горизонтальную асимптоту 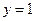 и вертикальную асимптоту
и вертикальную асимптоту  .
.
Дата добавления: 2014-11-13; просмотров: 387; Мы поможем в написании вашей работы!; Нарушение авторских прав |