Основные определения. Наглядные представления о непрерывности функции есть у всех, кто строил графики функций: если можно нарисовать график функции

Наглядные представления о непрерывности функции есть у всех, кто строил графики функций: если можно нарисовать график функции, заданной на некотором множестве, не отрывая карандаша от бумаги, то на этом множестве данная функция непрерывна. 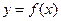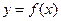Или другими словами: если величины и связаны друг с другом так, что малое изменение влечет за собой малое изменение , говорят, что непрерывно зависит от , то есть функция непрерывна.

Введем понятие приращение аргумента и приращения функции: – назовем приращением аргумента; – назовем приращением функции.

Определение 70.Функцию 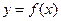называют непрерывной в точке , если:

1) она определена в точке ;

2) для любого сколь угодно малого положительного числа 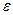найдется число 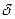такое, что из неравенства 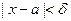вытекает неравенство (при этом ).

Краткая запись: ( непрерывна в точке ) ( ).

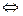Воспользуемся определением предела функции в точке; получим:

Определение 71.Функцию 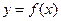называют непрерывной в точке , если предел функции в этой точке совпадает со значением функции в этой точке.

( непрерывна в точке ) ( ).

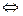Из Определение 71 следует замечательное свойство непрерывной функции: , то есть коммутативность двух операций: вычисление значения функции и вычисление предела.

Если обратиться к необходимому и достаточному условию существования предела функции в точке, получим:

Определение 72.Функцию 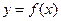называют непрерывной в точке , если:

1) она определена в точке ;

2) в этой точке существуют оба односторонних предела и ;

3) они равны между собой: = ;

4) они равны значению функции в этой точке .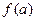

Воспользуемся определением 1 и понятиями приращения аргумента и приращения функции, получим:

Определение 73.Функция , определенная в точке , называется непрерывной в этой точке, если сколь угодно малому приращению аргумента соответствует бесконечно малое приращение функции.

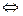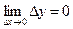( непрерывна в точке ) ( , где , ).

Все четыре определения непрерывности функции в точке равносильны между собой, но используются в различных ситуациях: Определение 70, Определение 71, и Определение 73 для доказательства непрерывности функции в точке, а Определение 72 – для классификации точек разрыва функций.

Пример 77.Докажите, что функция непрерывна при .

Доказательство:воспользуемся Определение 71 и рассмотрим , что совпадает с значит, непрерывна при .

Пример 78.Докажите, что линейная функция непрерывна при всех действительных .

Доказательство:пусть 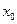– произвольное действительно число, рассмотрим приращение аргумента и соответствующее ему приращение функции: = = = ; тогда = = , значит, в силу Определение 73 функция непрерывна при всех действительных .

Определение 74.Функция 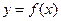называется непрерывной на некотором множестве 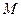, если она непрерывна в каждой точке этого множества.

Мы уже доказали, что линейная функция непрерывна при действительных , значит, для нее .