
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные определения. Определение 64. Любой интервал, содержащий точку , называется окрестностью точки
Определение 64.
 |
Любой интервал, содержащий точку
 , называется окрестностью точки
, называется окрестностью точки  . Симметричный интервал
. Симметричный интервал  при любом
при любом  называется
называется -окрестностью точки
-окрестностью точки  .
. 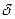 -окрестность точки
-окрестность точки  можно записать с помощью неравенства:
можно записать с помощью неравенства:  .
.
 |
Выколотая
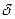 -окрестность точки
-окрестность точки  – это множество точек:
– это множество точек:  ,
,  или
или  .
.
Пусть функция 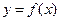 определена в некоторой выколотой окрестности точки
определена в некоторой выколотой окрестности точки  .
.
Определение 65.Число 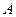 называется пределом функции
называется пределом функции 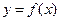 при
при  , стремящимся к
, стремящимся к  (или в точке
(или в точке  ), если для любого положительного числа
), если для любого положительного числа 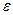 найдётся такое положительное число
найдётся такое положительное число 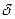 , что при всех
, что при всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству  , будет выполняться неравенство
, будет выполняться неравенство  .
.
Обозначение: 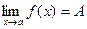 .
.
С помощью кванторов это определение запишем так:

Если число 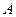 является пределом функции
является пределом функции  в точке
в точке  , то геометрически это означает, что график функции
, то геометрически это означает, что график функции  для
для 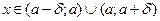 находится внутри прямоугольника, ограниченного прямыми
находится внутри прямоугольника, ограниченного прямыми  ;
; 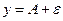 ;
;  ;
;  .
.
 Однако точка
Однако точка  (если в точке
(если в точке  функция
функция  определена) может как принадлежать, так и не принадлежать этому прямоугольнику (рис. 29).
определена) может как принадлежать, так и не принадлежать этому прямоугольнику (рис. 29).
Если число  устремить к нулю, то этот прямоугольник будет стягиваться к точке
устремить к нулю, то этот прямоугольник будет стягиваться к точке  , и, значит, когда точка
, и, значит, когда точка  стремится к точке
стремится к точке  , то точка
, то точка 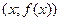 графика функции
графика функции  стремится к точке
стремится к точке  .
.
Пример 73.Докажите, что  .
.
Функция  определена в любой окрестности точки
определена в любой окрестности точки  . Неравенства
. Неравенства  ,
,  ,
,  будут выполняться для всех
будут выполняться для всех  , удовлетворяющих условию
, удовлетворяющих условию  . Таким образом,
. Таким образом,  , это и означает, что
, это и означает, что  .
.
Не для всякой функции, определённой в окрестности точки  , существует предел при
, существует предел при  . Например, функция
. Например, функция 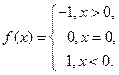
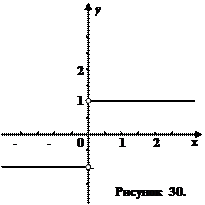 Эта функция (рис. 30) не имеет предела в точке
Эта функция (рис. 30) не имеет предела в точке  . (Докажите самостоятельно).
. (Докажите самостоятельно).
Дата добавления: 2014-11-13; просмотров: 651; Мы поможем в написании вашей работы!; Нарушение авторских прав |