
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Замечательные пределы
Докажем, что  (первый замечательный предел).
(первый замечательный предел).
Доказательство:  Рассмотрим единичную окружность. Предположим, что
Рассмотрим единичную окружность. Предположим, что  удовлетворяет неравенству
удовлетворяет неравенству  и обозначает радианную меру некоторого угла NOM. Рассмотрим треугольник OMN, OPN и сектор MON (рис. 30).
и обозначает радианную меру некоторого угла NOM. Рассмотрим треугольник OMN, OPN и сектор MON (рис. 30).
 ; (*)
; (*)
 ;
;
 ;
;  .
.
Подставив найденные выражения в (*), имеем: 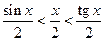
 , поскольку
, поскольку  при
при 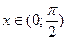 , то
, то 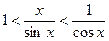 ;
;  . (**)
. (**)
 , следовательно,
, следовательно,  .
.
Замена  на
на 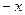 не нарушает неравенство (**). Поэтому оно справедливо и для
не нарушает неравенство (**). Поэтому оно справедливо и для  . Значит,
. Значит,  .
.
Рассмотрим несколько упражнений:
1)  .
.
2)  , где
, где  и при
и при 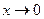 также и
также и  .
.
3) 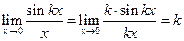 .
.
4)  , где
, где  и если
и если 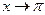 , то
, то  .
.
Рассмотрим второй замечательный предел и некоторые его обобщения: известно, что  . Если
. Если  , то
, то  , аналогично при
, аналогично при 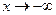 :
:  . Вообще,
. Вообще,  . Пусть
. Пусть  , тогда если
, тогда если  , то
, то  и мы получим:
и мы получим: 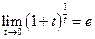 . Итак,
. Итак,  - второй замечательный предел. Рассмотрим некоторые следствия.
- второй замечательный предел. Рассмотрим некоторые следствия.
Если в равенстве  прологарифмировать левую и правую части, то получим
прологарифмировать левую и правую части, то получим  . Таким образом,
. Таким образом,  - третий замечательный предел.
- третий замечательный предел.
В равенстве  сделаем замену:
сделаем замену: 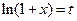 , тогда если
, тогда если 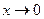 , то
, то  . Кроме того,
. Кроме того,  и
и  ; тогда получим
; тогда получим  или
или  - четвертый замечательный предел.
- четвертый замечательный предел.
Итак, замечательные пределы:

| 
| 
| 
|
Дата добавления: 2014-11-13; просмотров: 385; Мы поможем в написании вашей работы!; Нарушение авторских прав |